Back to the office after starting out early to make the long journey back to Brighton from Cardiff, all of which went smoothly for a change. I’ve managed to clear some of the jobs waiting for me on my return from the Christmas holidays so thought I’d take my lunch break and write a quick blog post. I hasten to add, however, that the title isn’t connected in any way with the speed of this morning’s train, which never at any point threatened causality.
What spurred me on to write this piece was an exchange on Twitter, featuring the inestimable Sean Carroll who delights in getting people to suggest physics for him to explain in fewer than three tweets. It’s a tough job sometimes, but he usually does it brilliantly. Anyway, the third of his tweets about the size of the (observable universe), and my rather pedantic reply to it, both posted on New Year’s Day, were as follows:
I thought I’d take the opportunity to explain in a little bit more detail how and why it can be that the size of the observable universe is significantly larger than what one naively imagine, i.e. (the speed of light) ×(time elapsed since the Big Bang) = ct, for short. I’ve been asked about this before but never really had the time to respond.
Let’s start with some basic cosmological concepts which, though very familar, lead to some quite surprising conclusions. First of all, consider the Hubble law, which I will write in the form
It’s not sufficiently widely appreciated that for a suitable definition of the recession velocity 
and distance 
, this expression is exact for any velocity, even one much greater than the speed of light! This doesn’t violate any principle of relativity as long as one is careful with the definition.
Let’s start with time. The assumption of the Cosmological Principle, that the Universe is homogeneous and isotropic on large scales, furnishes a preferred time coordinate, usually called cosmoloogical proper time, or cosmic time, defined in such a way that observers in different locations can set their clocks according to the local density of matter. This allows us to slice the four-dimensional space-time of the Universe into three spatial dimensions of one dimension of time in a particularly elegant way.
The geometry of space-time can now be expressed in terms of the Robertson-Walker metric. To avoid unnecessary complications, and because it seems to be how are Universe is, as far as we can tell, I’ll restrict myself to the case where the spatial sections are flat (ie they have Euclidean geometry). This the metric is:
![ds^{2}=c^{2}dt^{2} - a^{2}(t) \left[ d{r}^2 + r^{2}d\Omega^{2} \right]](https://s0.wp.com/latex.php?latex=ds%5E%7B2%7D%3Dc%5E%7B2%7Ddt%5E%7B2%7D+-+a%5E%7B2%7D%28t%29+%5Cleft%5B+d%7Br%7D%5E2+%2B+r%5E%7B2%7Dd%5COmega%5E%7B2%7D+%5Cright%5D&bg=000000&fg=B0B0B0&s=0&c=20201002)
Where 
is a four-dimensional interval 
is cosmological proper time as defined above, 
is a radial coordinate and 
defines angular position (the observer is assumed to be at the origin). The function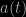 
is called the cosmic scale factor, and it describes the time-evolution of the spatial part of the metric; the coordinate of an object moving with the cosmic expansion does not change with time, but the proper distance of such an object evolves according to
The name “proper” here relates to the fact that this definition of distance corresponds to an interval defined instantaneously (ie one with 
). We can’t actually measure such intervals; the best we can do is measure things using signals of some sort, but the notion is very useful in keeping the equations simple and it is perfectly well-defined as long as you stay aware of what it does and does not mean. The other thing we need to know is that the Big Bang is supposed to have happened at at which point 
too.
If we now define the proper velocity of an object comoving with the expansion of the Universe to be
This is the form of the Hubble law that applies for any velocity and any distance. That does not mean, however, that one can work out the redshift of a source by plugging this velocity into the usual Doppler formula, for reasons that I hope will become obvious.
The specific case 
is what we need here, as that describes the path of a light ray (null geodesic); if we only follow light rays travelling radially towards or away from the origin, the former being of greatest relevance to observational cosmology, then we can set 
too and find:
Now to the nub of it. How do we define the size of the observable universe? The best way to answer this is in terms of the particle horizon which, in a nutshell, is defined so that a particle on the particle horizon at the present cosmic time is the most distant object that an observer at the origin can ever have received a light signal from in the entire history of the Universe. The horizon in Robertson-Walker geometry will be a sphere, centred on the origin, with some coordinate radius. The radius of this horizon will increase in time, in a manner that can be calculated by integrating the previous expression from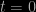 
to 
, the current age of the Universe:
For any old cosmological model this has to be integrated by solving for the denominator as a function of time using the Friedmann equations, usually numerically. However, there is a special case we can do trivially which demonstrates all the salient points. The matter-dominated Einstein- de Sitter model is flat and has the solution
so that
Plugging this into the integral and using the above definitions we find that in this model the present proper distance of an object on our particle horizon is
By the way, some cosmologists prefer to use a different definition of the horizon, called the Hubble sphere. This is the sphere on which objects are moving away from the observer according to the Hubble law at exactly the velocity of light. For the Einstein-de Sitter cosmology the Hubble parameter is easily found
Notice that velocities in this model are always decaying, so in it the expansion is not accelerating but decelerating, hence my comment on Twitter above. The apparent paradox therefore has nothing to do with acceleration, although the particle horizon does get a bit bigger in models with, e.g., a cosmological constant in which the expansion accelerates at late times. In the current standard cosmological model the radius of the particle horizon is about 46 billion light years for an age of 13.7 billion years, which is just 10% larger than in the Einstein de Sitter case.
There is no real contradiction with relativity here because the structure of the metric encodes all the requirements of causality. It is true that there are objects moving away from the origin at proper velocities faster than that of light, but we can’t make instantaneous measurements of cosmological distances; what we observe is their redshifted light. In other words we can’t make measurements of intervals with we have to use light rays, which follow paths with , i.e. we have to make observations down our past light cone. Nevertheless, there are superluminal velocities, in the sense I have defined them above, in standard cosmological models. Indeed, these velocities all diverge at 
. Blame it all on the singularity!
This figure made by Mark Whittle (University of Virginia) shows our past light cone in the present standard cosmological model:
If you were expectin the past light cone to look triangular in cross-section then you’re probably thinking of Minkowski space, or a representation involving coordinates chosen to resemble Minkowski space. Cosmological If you look at the left hand side of the figure, you will find the world lines of particles moving with the cosmic expansion labelled by their present proper distance which is obtained by extrapolating the dotted lines until they intersect a line parallel to the x-axis running through “Here & Now”. Where we actually see these objects is not at their present proper distance but at the point in space-time where their world line intersects the past light cone. You will see that an object on the particle horizon intersected our past light cone right at the bottom of the figure.
So why does the light cone look so peculiar? Well, I think the simplest way to explain it is to say that while the spatial sections in this model are flat (Euclidean) the four-dimensional geometry is most definitely curved. You can think of the bending of light rays shown in the figure as a kind of gravitational lensing effect due to all the matter in the Universe. I’d say that the fact that the particle horizon has a radius larger than 
is not because of acceleration but the curvature of space-time, an assertion consistent with the fact that the only familiar world model in which this effect does not occur is the (empty) purely kinemetic Milne cosmology, which is based entirely on special relativity.
In the Dark 