Archive for Charge Conjugation

CP Violation in Baryons

Posted in The Universe and Stuff with tags , , , , , , , on July 21, 2025 by telescoper

I was (pleasantly) surprised to learn a few weeks ago that I shall be teaching particle physics again next academic year. That means that I’ll have to update to the notes to reflect the latest news from CERN. Researchers from the LHCb collaboration have published evidence for CP violation in baryons. The paper is published in Nature here.

For those of you not up with the lingo, CP is an operator that combines C (charge-conjugation, i.e. matter versus anti-matter) and P (parity, i.e. inversion of coordinates). Parity has been known since the 1950s to be violated in weak interactions, so the weak nuclear force distinguishes between states of odd and even parity. CP violation was first demonstrated in the 1960s CP in the decays of neutral kaons resulted in the Nobel Prize  in 1980 for its discoverers Cronin and Fitch. CP violation has subsequeuntly been seen in many other meson decays.

But the mesons (consisting of a quark and an antiquark) are only half of the family of particles made from quarks; the others are the baryons which are made of three quarks (c.f. James Joyce’s “Three quarks for Muster Mark” in Finnegans Wake). Antibaryons consist of three antiquarks, but such are not mentioned in Finnegans Wake.

The baryons concerned in the LHCb experiment contain an up quark, a down quark and a beauty quark and were produced in proton–proton collisions at the Large Hadron Collider in 2011–2018. These baryons and antibaryons can decay via multiple channels. In one, a baryon decays to a proton, a positive K-meson and a pair of pions – or, conversely, an antibaryon decays to an antiproton, a negative K-meson and a pair of pions. CP violation should create an asymmetry between these processes, and the researchers found evidence of this asymmetry in the numbers of particles detected at different energies from all the collisions.

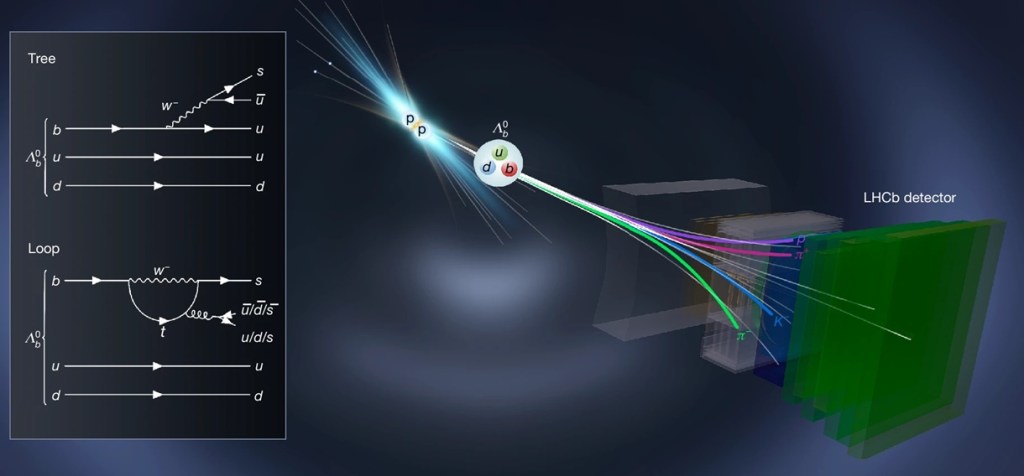
Figure 1 from https://doi.org/10.1038/s41586-025-09119-3

A problem with calculating the magnitude of this effect for baryons is that there is a contribution from the strong force – see the curly line indicating a gluon in the lower panel on the left above – and that is much harder to compute than a pure weak force (represented by the wavy lines indicating W– bosons. Yo will see that the tree and loop diagrams involve quark mixing, a process that allows quarks of different generations to couple via weak interactions; there is a buW vertex in the top panel and a tsW vertex in the bottom one. Given the uncertainties, it seems the results are consistent with the level of CP violation predicted in the Standard Model of particle physics.

The big question surrounding this result is whether it can account for the fact that our Universe – or at least our part of it -contains a preponderance of baryons over anti-baryons, so somehow the interactions going on during the Big Bang must have shown a preference for the former over the latter. This problem of baryogenesis is not explained in the Standard Model and, since these results are consistent with the Standard Model, the answer to that question is “no”…

Leave a comment »

Time will say nothing but I told you so…

Posted in The Universe and Stuff with tags , , , , , , , , , , , on November 20, 2012 by telescoper

A blog post at Nature News just convinced me that it’s time to post something about science for a change.

The paper (just published in Physical Review Letters) that inspired the Nature piece is entitled Observation of Time-Reversal Violation in the B0 Meson System and its publication gave me an excuse find the answer to a question that I’d wondered about for a while.

Although I’m not a real particle physicist, I have in the past been called upon to teach courses on particle theory (first at Nottingham and then here in Cardiff). One of the things I’ve emphasized in lectures on this subject is the importance of symmetries in particle physics and, perhaps even more important, the idea that symmetries you might think would hold in theory might actually be violated in the real world.

A good starting point is to think about parity. A parity transformation involves flipping the sign of all the spatial coordinates used to define a system; this operation involves the reflection of a system through the origin of the coordinate system so is connected with the notion of “handedness”. In quantum mechanics, an eigenstate of the parity operator P has two possible eigenvalues: +1 (even) or -1 (odd). One might expect this to be a “good”  quantum number in the sense that it is a quantity that is conserved during particle interactions. This is the case in many situations, but turns out not to be true in weak interactions; parity violation has been known about since the 1950s, in fact.

Another interesting symmetry relates to the operator C which represents charge conjugation. The charge-conjugation operation involves changing particles into anti-particles, e.g. inverting the electrical charge on the electron to make a positron.  Since the electron and positron seem to be identical apart from the different charge one suspects a general symmetry might apply here too. However, weak interactions are also known to violate C-symmetry (for example because under the action of C on a left-handed neutrino would turn into a left-handed anti-neutrino, which doesn’t exist in the standard model).

So if C and P aren’t conserved separately could the combined operation (CP)  represent a symmetry? CP acting on a left-handed neutrino would create a right-handed anti-neutrino, which does exist in the standard model so this seems a promising possibility. But no. CP is also violated in certain weak interactions. It’s always the weak interactions that mess things up, actually. Very irritating of them.

Now we come to the crux. In any model of particle interactions based on quantum field theory, the combination CPT has to be an exact symmetry. In this composite operator T represents time-reversal, so if you change particles into antiparticles, perform a parity flip, and run the clock backwards everything should look exactly the same. A corollary of this, since we know that CP is not an exact symmetry is that T can’t be either (otherwise it couldn’t restore the violation caused by CP). But how to test whether T is violated?

In fact, in lecturing on this topic I’ve always ended there and moved onto something else.  I’ve often wondered how one might test for T-violation but never arrived at an answer.  You can’t know everything.

Anyway, the answer is explained nicely in an explanatory article published with the paper. The B-mesons discussed in the paper are electrically neutral particles, but they can nevertheless exist as distinct particles and antiparticles. In this respect they are similar to their (lighter) cousins the neutral Kaons which played an important role in establishing CP violation back in the 60s.

Mesons comprise  a quark and an anti-quark bound together by the strong force. The neutral Kaon comprises a down quark and an anti-strange quark (or, if you prefer, a strange antiquark) whereas the anti-Kaon is an anti-down and a strange. Although these combinations have the same electrical charge (zero) they carry different overall quark flavour numbers and are therefore discernibly different. The B-mesons involve the bottom anti-quark and a down quark (and vice-versa for the anti-B).

The experiment analysed here, called BaBar and situated at the Stanford Linear Accelerator facility, detected B-mesons initially created as entangled pairs of B and anti-B each of which subsequently decays into either a CP-eigenstate or a pure flavour eigenstate.  To study T reversal, the physicists selected just those events in which  one meson decayed into a flavour state and the other  into a CP eigenstate.  These decays can happen in either order, but if T symmetry were to hold, then the decay rate of the second particle should not depend on whether the first particle decayed into a CP-eigenstate or a pure flavour state.  The experiment showed that there is a difference in these rates and therefore T-symmetry is broken. A time machine is not needed after all; the direction of time is supplied by the particles’ own spontaneous decays.

This isn’t an unexpected result. I reckon most particle physicists were pretty sure proof of T-violation would be found at some point. But it’s certainly a very clever experiment and it goes down as another success for the standard model of particle physics.

3 Comments »