In the Dark

The second in my sequence of posts tangentially related to talks at this meeting on Maximum Entropy and Bayesian Methods in Science and Engineering is inspired by a presentation this morning by Sylvia Wenmackers. The talk featured an example which was quite new to me called Norton’s Dome. There’s a full discussion of the implications of this example at John D. Norton’s own website, from which I have taken the following picture:

This is basically a problem in Newtonian mechanics, in which a particle rolls down from the apex of a dome with a particular shape in response to a vertical gravitational field. The solution is well-determined and shown in the diagram.

An issue arises, however, when you consider the case where the particle starts at the apex of the dome with zero velocity. One solution in this case is that the particle stays put forever. However it can be shown that there are other solutions in which the particle sits at the top for an arbitrary (finite) time before rolling down. An example could be for example if the particle were launched up the dome from some point with just enough kinetic energy to reach the top where it is momentarily at rest, but then rolls down again.

Norton argues that this problem demonstrates a certain kind of indeterminism in Newtonian Mechanics. The mathematical problem with the specified initial conditions clearly has a solution in which the ball stays at the top forever. This solution is unstable, which is a familiar situation in mechanics, but this equilibrium has an unusual property related to the absence of Lipschitz continuity. One might expect that an infinitesimal asymmetric perturbation of the particle or the shape of the surface would be needed to send the particle rolling down the slope, but in this case it doesn’t. This is because there isn’t just one solution that has zero velocity at the equilibrium, but an entirely family as described above. This is both curious and interesting, and it does raise the question of how to define a probability measure that describes these solutions.

I don’t really want to go into the philosophical implications of this cute example, but it did strike me that there’s a similarity with an interesting issue in cosmology that I’ve blogged about before (in different terms).

This probably seems to have very little to do with physical cosmology, but now forget about domes and think instead about the behaviour of the mathematical models that describe the Big Bang. To keep things simple, I’m going to ignore the cosmological constant and just consider how things depend on one parameter, the density parameter Ω₀. This is basically the ratio between the present density of the matter in the Universe compared to what it would have to be to cause the expansion of the Universe eventually to halt. To put it a slightly different way, it measures the total energy of the Universe. If Ω₀>1 then the total energy of the Universe is negative: its (negative) gravitational potential energy dominates over the (positive) kinetic energy. If Ω₀<1 then the total energy is positive: kinetic trumps potential. If Ω₀=1 exactly then the Universe has zero total energy: energy is precisely balanced, like the man on the tightrope.

A key point, however, is that the trade-off between positive and negative energy contributions changes with time. The result of this is that Ω is not fixed at the same value forever, but changes with cosmic epoch; we use Ω₀ to denote the value that it takes now, at cosmic time t₀, but it changes with time.

At the beginning, i.e. at the Big Bang itself,  all the Friedmann models begin with Ω arbitrarily close to unity at arbitrarily early times, i.e. the limit as t tends to zero is Ω=1.

In the case in which the Universe emerges from the Big bang with a value of Ω just a tiny bit greater than one then it expands to a maximum at which point the expansion stops. During this process Ω grows without bound. Gravitational energy wins out over its kinetic opponent.

If, on the other hand, Ω sets out slightly less than unity – and I mean slightly, one part in 10⁶⁰ will do – the Universe evolves to a state where it is very close to zero. In this case kinetic energy is the winner  and Ω ends up on the ground, mathematically speaking.

In the compromise situation with total energy zero, this exact balance always applies. The universe is always described by Ω=1. It walks the cosmic tightrope. But any small deviation early on results in runaway expansion or catastrophic recollapse. To get anywhere close to Ω=1 now – I mean even within a factor ten either way – the Universe has to be finely tuned.

The evolution of Ω  is neatly illustrated by the following phase-plane diagram (taken from an old paper by Madsen & Ellis) describing a cosmological model involving a perflect fluid with an equation of state p=(γ-1)ρc². This is what happens for γ>2/3 (which includes dust, relativistic particles, etc):

The top panel shows how the density parameter evolves with scale factor S; the bottom panel shows a completion of this portrait obtained using a transformation that allows the point at infinity to be plotted on a finite piece of paper (or computer screen).

As discussed above this picture shows that all these Friedmann models begin at S=0 with Ω arbitrarily close to unity and that the value of Ω=1 is an unstable fixed point, just like the situation of the particle at the top of the dome. If the universe has Ω=1 exactly at some time then it will stay that way forever. If it is perturbed, however, then it will eventually diverge and end up collapsing (Ω>1) or going into free expansion (Ω<1).  The smaller the initial perturbation,  the longer the system stays close to Ω=1.

The fact that all trajectories start at Ω(S=0)=1 means that one has to be very careful in assigning some sort of probability measure on this parameter, ust as is the case with the Norton’s Dome problem I started with. About twenty years ago, Guillaume Evrard and I tried to put this argument on firmer mathematical grounds by assigning a sensible prior probability to Ω based on nothing other than the assumption that our Universe is described by a Friedmann model.

The result we got was that it should be of the form

.

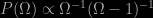I was very pleased with this result, which is based on a principle advanced by physicist Ed Jaynes, but I have no space to go through the mathematics here. Note, however, that this prior has three interesting properties: it is infinite at Ω=0 and Ω=1, and it has a very long “tail” for very large values of Ω. It’s not a very well-behaved measure, in the sense that it can’t be integrated over, but that’s not an unusual state of affairs in this game. In fact it is what is called an improper prior.

I think of this prior as being the probabilistic equivalent of Mark Twain’s description of a horse:

dangerous at both ends, and uncomfortable in the middle.

Of course the prior probability doesn’t tell usall that much. To make further progress we have to make measurements, form a likelihood and then, like good Bayesians, work out the posterior probability . In fields where there is a lot of reliable data the prior becomes irrelevant and the likelihood rules the roost. We weren’t in that situation in 1995 – and we’re arguably still not – so we should still be guided, to some extent by what the prior tells us.

The form we found suggests that we can indeed reasonably assign most of our prior probability to the three special cases I have described. Since we also know that the Universe is neither totally empty nor ready to collapse, it does indicate that, in the absence of compelling evidence to the contrary, it is quite reasonable to have a prior preference for the case Ω=1.  Until the late 1980s there was indeed a strong ideological preference for models with Ω=1 exactly, but not because of the rather simple argument given above but because of the idea of cosmic inflation.

From recent observations we now know, or think we know, that Ω is roughly 0.26. To put it another way, this means that the Universe has roughly 26% of the density it would need to have to halt the cosmic expansion at some point in the future. Curiously, this corresponds precisely to the unlikely or “fine-tuned” case where our Universe is in between  two states in which we might have expected it to lie.

Even if you accept my argument that Ω=1 is a special case that is in principle possible, it is still the case that it requires the Universe to have been set up with very precisely defined initial conditions. Cosmology can always appeal to special initial conditions to get itself out of trouble because we don’t know how to describe the beginning properly, but it is much more satisfactory if properties of our Universe are explained by understanding the physical processes involved rather than by simply saying that “things are the way they are because they were the way they were.” The latter statement remains true, but it does not enhance our understanding significantly. It’s better to look for a more fundamental explanation because, even if the search is ultimately fruitless, we might turn over a few interesting stones along the way.

The reasoning behind cosmic inflation admits the possibility that, for a very short period in its very early stages, the Universe went through a phase where it was dominated by a third form of energy, vacuum energy. This forces the cosmic expansion to accelerate; this means basically that the equation of state of the contents of the universe is described by γ<2/3 rather than the case γ>2/3 described above. This drastically changes the arguments I gave above.

Without inflation the case with Ω=1 is unstable: a slight perturbation to the Universe sends it diverging towards a Big Crunch or a Big Freeze. While inflationary dynamics dominate, however, this case has a very different behaviour. Not only stable, it becomes an attractor to which all possible universes converge. Here’s what the phase plane looks like in this case:

Whatever the pre-inflationary initial conditions, the Universe will emerge from inflation with Ω very close to unity.

So how can we reconcile inflation with current observations that suggest a low matter density? The key to this question is that what inflation really does is expand the Universe by such a large factor that the curvature radius becomes infinitesimally small. If there is only “ordinary” matter in the Universe then this requires that the universe have the critical density. However, in Einstein’s theory the curvature is zero only if the total energy is zero. If there are other contributions to the global energy budget besides that associated with familiar material then one can have a low value of the matter density as well as zero curvature. The missing link is dark energy, and the independent evidence we now have for it provides a neat resolution of this problem.

Or does it? Although spatial curvature doesn’t really care about what form of energy causes it, it is surprising to some extent that the dark matter and dark energy densities are similar. To many minds this unexplained coincidence is a blemish on the face of an otherwise rather attractive structure.

It can be argued that there are initial conditions for non-inflationary models that lead to a Universe like ours. This is true. It is not logically necessary to have inflation in order for the Friedmann models to describe a Universe like the one we live in. On the other hand, it does seem to be a reasonable argument that the set of initial data that is consistent with observations is larger in models with inflation than in those without it. It is rational therefore to say that inflation is more probable to have happened than the alternative.

I am not totally convinced by this reasoning myself, because we still do not know how to put a reasonable measure on the space of possibilities existing prior to inflation. This would have to emerge from a theory of quantum gravity which we don’t have. Nevertheless, inflation is a truly beautiful idea that provides a framework for understanding the early Universe that is both elegant and compelling. So much so, in fact, that I almost believe it.