Archive for electrostatics

A Question of Images

Posted in Cute Problems, mathematics, The Universe and Stuff with tags , on May 10, 2023 by telescoper

Today I gave a revision lecture/tutorial for my module Advanced Electromagnetism. With the Examination Period starting on Friday, that was the last class I will do for that. One of the topics I’ve been asked to cover in revision was the Method of Images for electrostatics. Preparing for the class I came across this cute problem which I thought I’d share here:

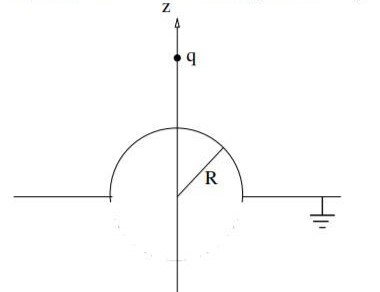
The question concerns a charge +q placed at a distance d as shown above an infinite earthed conducting plane distorted by the presence of a hemispherical bulge with radius R.

  1. Using the method of images, or otherwise, calculate the potential at an arbitrary point above the conducting surface. (HINT: you need three image charges)
  2. Find the magnitude and direction of the electrostatic force on the charge.

If you’re feeling keen you might also find what fraction of the total induced on the conductor is on the hemispherical part.

Answers through the comments box please!

Well, nobody posted an answer so here’s an outline solution.

To solve this problem you need three image charges: one is of charge – q at z=-d to make the plane an equipotential. For an isolated sphere you need a charge of -qR/d at z=-R^2/d  (the inverse point of the sphere). But this charge also has an effect on the plane, which you need to correct by placing another image charge of +qR/d at z=-R^2/d. That is, the solution for the potential is due to the original charge plus three image charges. Then the potential is just the sum of four point charges.

You can differentiate the answer to the first bit to get the force, or you could work out the force on the original charge directly by adding the forces in the z-direction from the three image charges, it being obvious by symmetry that there is no other component of the force. For d>R this results in a force which is downward, so the charge is pulled towards the conductor. I’ll leave that as an exercise!

4 Comments »

A Question of Electrostatic Repulsion

Posted in Cute Problems, The Universe and Stuff with tags , on March 7, 2023 by telescoper

It’s been a while since I posted a question in the Cute Physics Problems folder so I thought I’d offer this one. It’s not particularly hard, but I think it’s quite instructive.

A thin spherical shell of radius r carrying a charge Q spread uniformly with constant surface density is split into two equal halves by a narrow planar cut passing through the centre as shown in the detailed diagram below:

 

Calculate the force arising from electrostatic repulsion between the two hemispherical shells, expressing your answer in terms of Q and r in SI units.

Answers through the Comments Box please. First correct answer wins a tomato*

*subject to availability

9 Comments »

A Guest Paradox

Posted in Cute Problems, The Universe and Stuff with tags , , , on February 9, 2018 by telescoper

Here’s a short guest post by my old friend Anton. As usual, please feel free to discuss the paradox through the comments box!

–0–

I thought of a physics paradox the other day and Peter has kindly granted me a guest post here about it, as follows. Consider a homogeneous isotropic closed universe as described by general relativity. Let it contain a uniform density of a single species of electrically charged particle, so that this universe has a net charge. The charged particle density is sufficiently low, however, that the perturbation from the regular uncharged metric is negligible. Since this universe is homogeneous and isotropic the electric field in it is everywhere zero. BUT if I consider a conceptual 3-dimensional sphere, small enough for space-time curvature to be neglected, then it contains a finite amount of electric charge, and therefore by Gauss’ theorem a nonzero electric field points out of it at every point on its surface. This contradicts the zero-field conclusion based on the metric.

Here are three responses (one my own) and my further responses to these, in brackets:

  1. In a closed universe it is not clear what is the outside and what is the inside of the sphere, so Gauss’ law is not trustworthy (tell this to a local observer!);
  2. the electric field lines due to the charges inside this (or any) conceptual sphere wrap round the universe an infinite number of times (this doesn’t negate Gauss’ theorem!);
  3. the curved rest of the Universe actually adds a field that cancels out the field in your sphere (neither does this negate Gauss’ theorem!)

23 Comments »

A Problem of Capacitors

Posted in Cute Problems, The Universe and Stuff with tags , , on April 3, 2014 by telescoper

Time for another entry in the Cute Problems  category. I’ve been teaching a course module  in theoretical physics this term so here’s one that my students should find a doddle…

A spherical capacitor consists of an outer conducting sphere of fixed radius b and a concentric inner conducting sphere whose radius a can be varied. The space between the spheres is filled with air which has a breakdown electric field strength E0. What are the greatest achievable values for (i) the potential difference between the spheres, and (ii) the electrostatic energy stored in the capacitor?

Answers via the comments box please.

1 Comment »

Methods of Images

Posted in Biographical, Cute Problems, Education with tags , , , , on January 29, 2014 by telescoper

I’ve had a very busy day today including giving a lecture on Electrostatics and the Method of Images and, in an unrelated lunch-hour activity, filing my tax return (and paying the requisite bill). The latter was the most emotionally draining.

With no time for a proper post, I thought I’d give some examples of the images produced by yesterday’s graduands, including some who used a particular approach called the Method of Selfies. Unfortunately some of these are spoiled by having a strange bearded person in the background.

But first you might like to try the following example using the actual Method of Images:

Given two parallel, grounded, infinite conducting planes a distance a apart, we place a charge +q between the plates, a distance x from one of them. What is the force on the charge?

This is, in fact, from Griffiths, David J. (2007) Introduction to Electrodynamics, 3rd Edition; Prentice Hall – Problem 3.35.

Solutions via the comments box as usual, please.

And now here are some of the official pictures from yesterday

9

1

2

3

4

5

6

7

8

6 Comments »

The Problem of the Charged Bubble

Posted in Cute Problems with tags , , , on November 21, 2012 by telescoper

Fun physics problem time. I like problems that combine different concepts, so here’s one such from Ye Olde Booke of Cavendish Problems, in a multiple-choice format. It’s not particularly hard, but I like it anyway…

A soap bubble – the film may be taken to be a conductor – of radius 10 mm and surface tension 0.02 N/m is charged by momentarily connecting it to an electrode at 6 kV. How does the radius of the bubble change?

PS. Americans, please note the correct usage of “momentarily”…

15 Comments »