It seems to be a common misapprehension that the energy released by the supermassive black holes in, for example, active galactic nuclei is in the form of Hawking radiation. It isn’t. Hawking radiation is only significant for black holes of very low mass. The radiation produced around supermassive black holes is due to the extremely high density and temperate of matter falling into the black hole through an accretion disk not due to the evaporation of the black hole itself. Hawking radiation has never been experimentally detected.
Hawking showed that the a black hole will produce black-body radiation with a temperature, the Hawking Temperature, given by TH in a beautiful formula below that brings together constants relating to gravity, statistical mechanics, quantum theory and relativity:
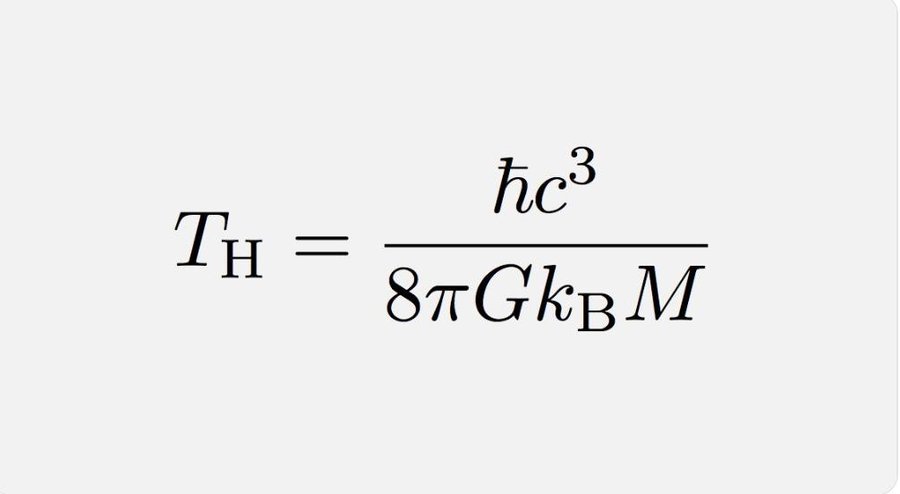
You can see that the Hawking Temperature is inversely proportional to the mass of the black hole M so is largest for very small black holes. In fact for a black hole with mass of order that of the Moon, the Hawking Temperature is just 3 Kelvin. Since the Universe is bathed in cosmic radiation with this temperature, such a black hole would not evaporate at all because it would absorb as much radiation as it emits by the Hawking mechanism as would any black hole of mass greater than this. The Hawking temperature for a supermassive black hole is many orders of magnitude lower than this, so Hawking radiation is completely irrelevant.
Notice that if a black hole does start to evaporate then its mass begins to decrease. Its Hawking temperature therefore increases so its mass decreases even more quickly. In the end the mass gets so low and the temperature so high that the black hole effectively explodes. Nobody really knows how to describe the final stage as it relies on physics we don’t understand.
Anyway, this all reminds that years ago I set an examination question that involved applying the Hawking formula above to calculate the lifetime of a black hole of mass M. It’s not too hard to show that it scales as M-3. Another part of the question asked: what is the mass of a black hole whose Hawking Temperature is room temperature (say 300 K), what would be the Schwarzschild radius of such a black hole, and what would be its lifetime?
I’ll leave it to my readers to plug the numbers into the Hawking formula above to derive the mass, etc. Please submit your answers through the comments box below. The first correct entry does not win a prize, not even a joke Peace Prize.
For a laugh I asked Google for the answer. Here is the AI summary:
Bonus marks for pointing out everything that’s wrong in this summary.