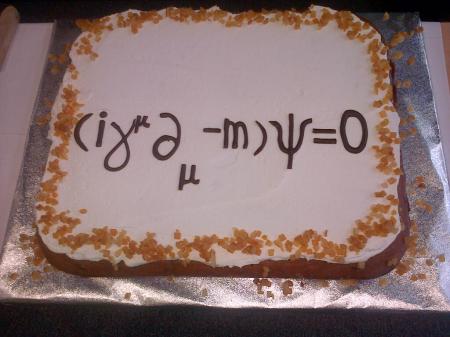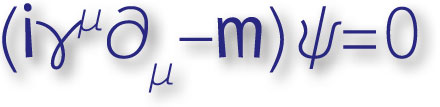Archive for mathematics

« Older Entries

A month to go

Posted in Artificial Intelligence, Biographical, Education, mathematics, Maynooth with tags , , , , , on November 25, 2025 by telescoper

I’ve been a bit preoccupied these recent weeks so it was with a shock that I realised that we’re into Week 9, which means just four weeks (including this one) until the end of term and just a month before Christmas. Teaching finishes here in Maynooth on Friday 19th December, but I don’t have any lectures on Fridays so in my case it will finish the day before (with a tutorial). I don’t know how many students will be there, but the module concerned is my 4th year Mathematical Physics module and the students are very hard-working, so I think most will attend. After such a busy term I’m sure that they will need a break as much as I will.

I had to rejig the schedule for both modules I am teaching this semester to accommodate the introduction of in-class tests to replace take-home assignments (for reasons I outlined here). I’ve also been handing out voluntary exercises for practice, not counting towards the module mark but for formative reasons. Both modules are mathematical in nature, and I think the best way to learn mathematics is by doing it…

Despite the changes with respect to last year, I am still roughly on track. In my Engineering Mathematics module I’ve just finished Laplace transforms, and will start Fourier methods tomorrow. With the mathematical physicists, I am in the middle of complex analysis, having done complex differentiation and conformal mappings and starting complex integration next week.

I still have a couple more class tests to get through. On the positive side, the students are turning up for them and have expressed approval for the fact that they don’t have compulsory homework to do off-campus. This form of assessment is undoubtedly harder work for the students, it’s also better preparation for the examination that take-home assignments.

We’ve just received the draft examination timetable for January, and I’m pleased that both of the examinations for which I am responsible will take place quite early in the examination period (on 12th and 15th January, respectively) so I should be able to get them corrected in time to have a break for some research before teaching resumes at the start of February.

Leave a comment »

Testing Times

Posted in Artificial Intelligence, Education, mathematics, Maynooth with tags , , , , on October 17, 2025 by telescoper

As it was foretold, I conducted my first set of my new-style in-class tests this week. These tests, as I mentioned a while ago,  were introduced because of concerns about the integrity of the coursework element of my modules in the light of improvements in Generative AI.

The main events – one for each of my modules – were both yesterday, but one student couldn’t make it at the scheduled time (for good reasons) so I set a special test this morning, which is now over. Because access to the internet is not allowed these tests are invigilated.

It’s been quite a while since I was last required to invigilate a full examination. I think it was back in Nottingham days, actually. I never enjoyed this task even though I took work to do it wasn’t really possible to do much as one had to keep one’s eyes on the students. Crosswords could be done; these are good in this situation because you can solve a few clues at a time. It was disappointing if I happened to take one that was easy enough to do quickly, as there was little to stave off the boredom after completing it. Other things I used to do included counting the number of right-handed and left-handed students, though I never did any detailed statistical analysis of the results.

Anyway, my recent class tests were a bit different. Designed to fit in a lecture slot of 50 minutes duration, they were much shorter than traditional end-of-year exams. They were also “open-book” style, so students could bring anything on paper that they wanted. Phones and laptops were, however, forbidden. During these tests I just sat quietly with my laptop getting some work done, with an occasional glance at the students. It was actually nice to be locked away like this with no disturbance. Time passed very quickly, actually, though perhaps not as quickly as it did for the students taking the tests.

When I first told the students that the tests would be “open-book”, I think they all assumed that would make them easy. I don’t think that was the case, however, as the questions are designed so that the answers can’t be obtained immediately by looking them up in a textbook. Also, having things on paper rather than in your head does slow you down. I’ve never seen much point in examinations as speed tests. I designed this week’s tests so that the questions could be done in about 30 minutes, but the formal duration was 50 minutes. I encouraged students who finished early to use the remaining time to check their work, but some did leave early.

This new regime also meant I had number of teaching sessions without the exertion of having to do any actual teaching, which was nice. The downside is, of course, that I now have stacks of class tests to correct. That will be payback time.

I won’t know how well the students have coped until I have got their grades, but informal feedback was that they seemed reasonably content with the new method of assessment. I’ll be doing the next ones in about three weeks.

Leave a comment »

Quarter-Term – Testing Time

Posted in Education, mathematics, Maynooth with tags , , , on October 13, 2025 by telescoper

I’ve just noticed that three teaching weeks have passed and we’re already into the fourth. Tempus fugit. Both the modules I am lecturing this semester are divided into four chunks of approximately equal size. For example, MP469 Differential Equations and Complex Analysis splits into: Ordinary Differential Equations; Partial Differential Equations; Complex Functions and Derivatives; and Complex Integration. Though technically not on the syllabus, I also do couple of lectures on Conformal Mappings because I think they’re cool.

As I mentioned a while ago,  I am concerned about the integrity of the coursework element of these modules in the light of improvements in Generative AI. Only a couple of years ago GenAI could not solve the sort of problems I set for homework, but now it generally can. I don’t altogether object to people applying artificial intelligence to solve mathematical problems, but the main issue is that it does make mistakes. Moreover, instead of saying “sorry I can’t solve that problem” it will generally present a superficially plausible but incorrect solution. Although students will probably use GenAI for problem-solving, I think it is important that they learn to do such problems themselves, otherwise they won’t know whether the solution coughed up by the algorithm is correct or not.

The only way to learn mathematics is by doing it. If students get GenAI to do the mathematics for them, then they won’t learn it. In the past we have given marks for coursework (usually 20% of the module mark) mainly to encourage students to do them. Students who don’t bother to do these exercises generally do badly in the final exam (80%).

For these reasons I am moving the assessment from weekly homework sheets – which could be tackled with AI – to supervised in-class tests for which students can use notes on paper, but not laptops or phones. I will of course give examples for the students to have a go at themselves, and I will give feedback on their attempts, but they will not contribute to the module score. Another advantage of this approach is that students won’t have to do so much work against deadlines outside of class.

What I’ve decided to do is have one class test for each of the four sections of each module. Given that we’re about a quarter of the way through the term, it’s time for the first ones. This week there will be a class test on Ordinary Differential Equations. I’ve never been enthusiastic about examinations being speed tests, so I’ve decided to set problems to be done in a 50-minute session which would be expected to take about 30 minutes in a formal end-of-term examination.

I have to make a short work-related trip that will keep me away on Wednesday, but I’ve already written the test questions, and will make arrangements for someone to supervise the tests if for some reason I don’t make it back to Maynooth on time…

Anyway, although we’ve been teaching for three weeks I still have to check my calendar to remember which room I’m supposed to go to before every lecture. Perhaps by Christmas I will have learned them off by heart…

1 Comment »

Back to Teaching and Coping with GenAI

Posted in Artificial Intelligence, Education, mathematics, Maynooth with tags , , , , on September 21, 2025 by telescoper

Summer is well and truly over: it’s a chilly day in Maynooth; the Autumnal Equinox takes place tomorrow; and tomorrow I return to teaching at Maynooth University. So begins my antepenultimate academic year as a university teacher.

I’ve often remarked how the academic year at Maynooth is largely defined by the astronomical phenomena of the equinoxes and solstices. This year demonstrates this perfectly: Semester 1 lectures for undergraduates begin tomorrow (22nd September), the day of the Autumnal equinox; they end on Friday 19th December with the Winter Solstice on 21st. The half-term study break coincides with Samhain, a cross-quarter day. It’s all refreshingly pagan.

This time last year, having been away on sabbatical the year before, I was preparing to teach two new modules. I have those two again this year so this year should be a bit easiest than last year. I still have to get everything sorted out, though, including setting up my Moodle pages and preparing the materials, which is what I’ve been doing today.

The timetable for my Engineering Mathematics (EE206 Differential Equations and Transform Methods) module has not changed, so my first lectures on that (a double session) are not until Tuesday. I’m also doing MP469 Differential Equations and Complex Analysis for 4th Year Mathematical Physics students again, but the lecture times for that have changed. That is because, as a consequence of the merger of the Departments of Theoretical Physics and Experimental Physics to form a single Department of Physics, times have been coordinated as far as possible to ensure that Physics students can have flexibility in their choice of theoretical or experimental-based modules. The Engineering Mathematics module has not changed because the times for those lectures are such as to fit with the needs of the Department of Engineering, rather than Physics.

The upshot of all this is that my first lecture of the new term is for MP469, tomorrow afternoon at 2pm and my second is also MP469, at 11am on Tuesday. This means that I have three hours of lectures on Tuesdays this term, but at least that makes it possible to have a day without teaching (Wednesday).

You will notice that both the modules I am teaching this term are mathematical in nature. I have been concerned about the integrity of the coursework element of these modules in the light of improvements in Generative AI. Only a couple of years ago GenAI could not solve the sort of problems I set for homework, but now it generally can – especially for EE206. I don’t altogether object to people applying artificial intelligence to solve mathematical problems, but the issue is that it does make mistakes. Moreover, instead of saying “sorry I can’t solve that problem” it will generally present a superficially plausible but incorrect solution. Although students will probably use GenAI for problem-solving, I think it is important that they learn to do such problems themselves, otherwise they won’t know whether the solution coughed up by the algorithm is correct or not. That way lies disaster.

The only way to learn mathematics is by doing it. If students get GenAI to do the mathematics for them, then they won’t learn it. In the past we have given marks for coursework (usually 20% of the module mark) mainly to encourage students to do them. Students who don’t bother to do these exercises generally do badly in the final exam (80%).

For these reasons I am moving the assessment from weekly homework sheets – which could be tackled with AI – to supervised in-class tests for which students can use notes on paper, but not laptops or phones, just like they would in the final examination. I will of course give examples for the students to have a go at themselves, and I will give feedback on their attempts, but they will not contribute to the module score. Another advantage of this approach is that students won’t have to do so much work against deadlines outside of class.

Anyway, that’s the approach I am going to try. I’d be interested to hear what others are doing to deal with GenAI. The Comments Box is at your disposal.

P.S. There is a rumour circulating that The Rapture will occur on Tuesday 23rd September, but it is as yet unclear whether this will happen before, during, or after the lectures I am due to give on that day.

9 Comments »

The 2025 Leaving Certificate Mathematics Papers

Posted in Education, mathematics with tags , , on June 7, 2025 by telescoper

As I mentioned a few days ago, examinations for the 2025 school Leaving Certificate are under way. One of the interesting things about the Irish system is that the examination papers are put up online immediately after the examinations. Students took their first paper in Mathematics (either Ordinary or Higher level) on Friday (yesterday), and there has been some reaction.

Anyway, I thought I’d share the papers here so you can see what you think. Paper 2 is on Monday 9th June, so I’ll add those papers then.

LC003GLP100EVDownload
LC003ALP100EVDownload

They look reasonable to me. The thing that strikes me about them is that they are much more structured than the A-level mathematics examinations I took way back in 1981.

Comments are welcome through the box below.

Update: As promised here are the Papers 2:

LC003GLP200EVDownload
LC003ALP200EVDownload

Reaction to Paper 2 of Higher Mathematics is that it was more challenging than Paper 1.

4 Comments »

The Leaving

Posted in Biographical, Education, mathematics, Maynooth with tags , , , , , on June 4, 2025 by telescoper

Today is not only a significant date for me (in more ways than one), but it’s important for many young people in Ireland because the Junior Certificate and Leaving Certificate examinations both start today, so the first thing I need to do is wish everyone starting their examinations the very best of luck!

Among other things, the results of the leaving certificate examinations are important for September’s university admissions. This year the grade inflation that occurred during the pandemic years will be reduced, though it is not yet clear how. Whatever happens is likely to have a big impact on student recruitment to third-level institutions.

In the system operating in England and Wales the standard qualification for entry is the GCE A-level. Most students take A-levels in three subjects, which gives them a relatively narrow focus although the range of subjects to choose from is rather large. In Ireland the standard qualification is the Leaving Certificate, which comprises a minimum of six subjects, with many students taking more than this. This gives students a broader range of knowledge at the sacrifice (perhaps) of a certain amount of depth; it has been decreed for entry into this system that an Irish Leaving Certificate subject counts as about 2/3 of an A-level subject for admissions purposes, so Irish students do the equivalent of at least four A-levels, and many do more than this. It’s also worth noting that all students have to take Mathematics at Leaving Certificate level.

One can choose to do Leaving Certificate subjects at Ordinary or Higher level and there’s quite a big difference between the two, especially in Mathematics (of which more below).

Overall I prefer the Leaving Certificate over the UK system of A-levels, as the former gives the students a broader range of subjects than the latter (as does the International Baccalaureate). I would have liked to have been allowed to take at least one arts subject past O-level, for example.

For University admissions points are awarded for each paper according to the marks obtained and then aggregated into a total CAO points, CAO being the Central Applications Office, the equivalent of the UK’s UCAS. This means, for example, that our main Science pathway at Maynooth allows students to study Physics without having done it at Leaving Certificate level. This obviously means that the first year has to be taught at a fairly elementary level, but it has the enormous benefit of allowing us to recruit students whose schools do not offer Physics.

There is however a big problem with Mathematics. It was decided some years ago that students would get 25 extra CAO points if they got a mark of at least 40% in Higher Mathematics. This has led to more students taking the subject, which is good, but there are signs that this may have led to a decline in standards. If, for example, the marking is such that a fixed proportion of students get the top grade but more weaker students take the examination, that means that standards fall at the top end. For more discussion, see here.

Anyway, our Theoretical Physics & Mathematics course requires a good result in Higher Mathematics for entry. Will changes to the marking of Higher Mathematics this year make it harder for students to make the grade? We’ll just have to wait and see.

Moreover, since the pandemic struck, students have been able to choose to answer questions from a limited range of sections on the mathematics examination papers. That means that students can get very high grades despite knowing nothing about a big chunk of the syllabus. That matters most for subjects that require students to have certain skills and knowledge for entry into University, such as Physics. I taught part of our first year Mathematical Physics course in Maynooth for about 5 years. It was noticeable how the fraction that were comfortable with basic differentiation and integration was falling. Will this trend accelerate? Again, we’ll just have to wait and see…

1 Comment »

Beautiful Equations

Posted in Biographical, mathematics, The Universe and Stuff with tags , , , , on February 25, 2025 by telescoper

I did a lecture today about the Dirac Equation (which is almost 100 years old, having been first presented in 1928). You might think this is a difficult topic to lecture on, but it’s really a piece of cake:

This reminds me that a a while ago I posted about an interesting article on the BBC website that discussed the way mathematicians’ brains appear to perceive “beauty”. A (slightly) more technical version of the story can be found here. According to functional magnetic resonance imaging studies, it seems that beautiful equations excite the same sort of brain activity as beautiful music or art.

The question of why we think equations are beautiful is one that has come up a number of times on this blog. I suspect the answer is a slightly different one for theoretical physicists compared with pure mathematicians. Anyway, I thought it might be fun to invite people offer suggestions through the comments box as to the most beautiful equation along with a brief description of why.

I should set the ball rolling myself, and I will do so with the Dirac Equation:

dirac_equation

This equation is certainly the most beautiful thing I’ve ever come across in theoretical physics, though I don’t find it easy to articulate precisely why. I think it’s partly because it is such a wonderfully compact fusion of two historic achievements in physics – special relativity and quantum mechanics – but also partly because of the great leaps of the imagination that were needed along the journey to derive it and my consequent admiration for the intellectual struggle involved. I feel it is therefore as much an emotional response to the achievement of another human being – such as one feels when hearing great music or looking at great art – as it is a rational response to the mathematical structure involved. But it’s not just that, of course. The Dirac Equation paved the way to many further developments in particle physics. It seems to encapsulate so much about the behaviour of elementary particles in so few symbols. Some of its beauty derives from its compactness- it uses up less chalk in a mathematical physics lecture.

Anyway, feel free to suggest formulae or equations, preferably with a brief explanation of why you think they’re so beautiful.

P.S. Paul Dirac was my (academic) great-grandfather.

4 Comments »

Teaching Transforms

Posted in Education, History, Maynooth, The Universe and Stuff with tags , , , , , on November 21, 2024 by telescoper

We’re about two-thirds of the way into the Autumn Semester here at Maynooth and, by a miracle, I’m just about on schedule with both the modules I’m teaching. It’s always difficult to work out how long things are going to need for explanation when you’re teaching them for the first time.

One of the modules I’m doing is Differential Equations and Transform Methods for Engineering Students. I’ve been on the bit following the “and” for a couple of weeks already. The first transform method covered was the Laplace transform, which I remember doing as a physics undergraduate but have used only rarely. Now I’m doing Fourier Series, as a prelude to Fourier transforms.

As I have observed periodically, the differential equations and transform methods are not at all disconnected, but are linked via the heat equation, the solution of which led Joseph Fourier to devise his series in Mémoire sur la propagation de la chaleur dans les corps solides (1807), a truly remarkable work for its time that inspired so many subsequent developments.

In the module I’m teaching, the applications are rather different from when I taught Fourier series to Physics students. Engineering students at Maynooth primarily study electronic engineering and robotics, so there’s a much greater emphasis on using integral transforms for signal processing. The mathematics is the same, of course, but some of the terminology is different from that used by physicists.

Anyway I was looking for nice demonstrations of Fourier series to help my class get to grips with them when I remembered this little video recommended to me some time ago by esteemed Professor George Ellis. It’s a nice illustration of the principles of Fourier series, by which any periodic function can be decomposed into a series of sine and cosine functions.

This reminds me of a point I’ve made a few times in popular talks about astronomy. It’s a common view that Kepler’s laws of planetary motion according to which which the planets move in elliptical motion around the Sun, is a completely different formulation from the previous Ptolemaic system which involved epicycles and deferents and which is generally held to have been much more complicated.

The video demonstrates however that epicycles and deferents can be viewed as the elements used in the construction of a Fourier series. Since elliptical orbits are periodic, it is perfectly valid to present them in the form of a Fourier series. Therefore, in a sense, there’s nothing so very wrong with epicycles. I admit, however, that a closed-form expression for such an orbit is considerably more compact and elegant than a Fourier representation, and also encapsulates a deeper level of physical understanding. What makes for a good physical theory is, in my view, largely a matter of economy: if two theories have equal predictive power, the one that takes less chalk to write it on a blackboard is the better one!

Anyway, soon I’ll be moving onto the complex Fourier series and thence to Fourier transforms which is familiar territory, but I have to end the module with the Z-transform, which I have never studied and never used. That should be fun!

1 Comment »

Midpoint at Maynooth

Posted in Biographical, Education, mathematics, Maynooth with tags , , , , on November 11, 2024 by telescoper

Amid all the excitement last week I forgot that it was the sixth teaching week of the Semester. That means that we’re now past the halfway point. Among other things that meant that examination papers were due in on Friday (8th November). That means two papers for each module I’m teaching, one to be sat in January and another for the repeat opportunity in August, so that’s four altogether.

I always find setting examination questions very difficult. In theoretical physics we want to stretch the stronger candidates at the same time as allowing the weaker ones to show what they can do. It’s a perennial problem how to make the questions neither too easy nor too difficult, but it is compounded this time by the fact that I’m teaching two modules for the very first time so judging the right level is tricky.

Another issue is that I’m once again in a situation in which I have to set examination papers without having taught all the material. At least I’ve covered the first half of the content so I have some idea of what the students found difficult, but that’s not the case for the second half. It should be a bit easier next year once I’ve experience of covering the whole syllabus. Assuming, of course, that I’m teaching the same modules again next year, which is by no means guaranteed…

I’m teaching a module on Differential Equations and Complex Analysis for 4th year students and just about ready to switch to the part that comes after the and. I taught a bit of Complex Analysis when I was at Sussex and I’m quite looking forward to it, although it does pose a particular challenge. Some of the class are doing a Double Major in Theoretical Physics and Mathematics, and have done quite a lot of Complex Analysis before, while others are doing a Single Major in Theoretical Physics and haven’t really done any. I have to somehow find a way to satisfy these two different groups. The only way I can think of to do that is to teach the subject as a physicist rather than a pure mathematician, with an emphasis on examples and real-world applications rather than in the abstract. We’ll see how this works out over the next few weeks.

P.S. On the subject of Complex Analysis, I just remembered this post from a few years ago.

2 Comments »

Sturm und Liouville

Posted in Biographical, Education, mathematics with tags , , , , , on October 4, 2024 by telescoper

It’s Friday afternoon at the end of Week 2 here at Maynooth so I’ve now completed the 4th lecture of my 4th-year module Differential Equations and Complex Analysis. We’ve now in the section of Sturm-Liouville Theory. I’ve never taught this module before and, as always, teaching a new thing reminds me of all the things I had forgotten since I was a student. In this particular case, I still have the notes I took when I was studying this topic as an undergraduate. It’s scary to think the notes shown above were written by me 40 years ago!

Anyway, as I like to know something about the people behind the names, Sturm-Liouville Theory is named after Jacques Charles François Sturm (1803–1855)* and Joseph Liouville (1809–1882). Contrary to what I’d always assumed, Sturm was not German but was born in Geneva, which is now in Switzerland but which had been annexed by revolutionary France in 1798 so technically speaking he was born in France. Liouville was born in Saint-Omer, near Calais, which to my knowledge has never been part of Switzerland but has been part of the Spanish Netherlands.

*Given the dates, Sturm must have collaborated with Liouville after his earlier work with Drang…

2 Comments »

« Older Entries