Archive for Natural Units

Back to Teaching

Posted in Biographical, Education, Maynooth, The Universe and Stuff with tags , , , on February 4, 2025 by telescoper

After yesterday’s holiday it was back to teaching full-time this morning with the first lecture of my module on Particle Physics. I just about managed to get everything ready in time for the teaching session at 1pm which, because it was an introductory lecture with lots of pictures, I decided to do via powerpoint rather than my usual chalk-and-talk. That didn’t get off to a very good start because the podium PC in my room had decided to do a Windows update just before I started and I had to wait for that to finish before I could show my slides. I suppose that happened because this was the first day of teaching after a lengthy break so nobody had used the room recently.

Most of the lecture was devoted to introducing natural units, which I intend to use throughout the module, like I have on previous occasions I have taught this sort of material for reasons I explained here. The last time I taught particle physics was some 15 years ago, so I had to update some things, especially the picture of the components of the standard model to include the Higgs. After extensive research (by which I mean looking at wikipedia) I found the above; the Higgs is on the right. Unfortunately the particle masses – which reveal themselves if you click on the image above – are not given in natural units, but have pesky factors of c-squared in them. You can’t have everything.

The bit I’m looking forward to most is doing the Dirac Equation which, years ago when I was at Sussex, was once the subject of a cake:

That particular cake was a lemon drizzle cake which unfortunately is not one of the flavours represented in the standard model.

4 Comments »

The Joy of Natural Units

Posted in The Universe and Stuff with tags , , , on March 5, 2010 by telescoper

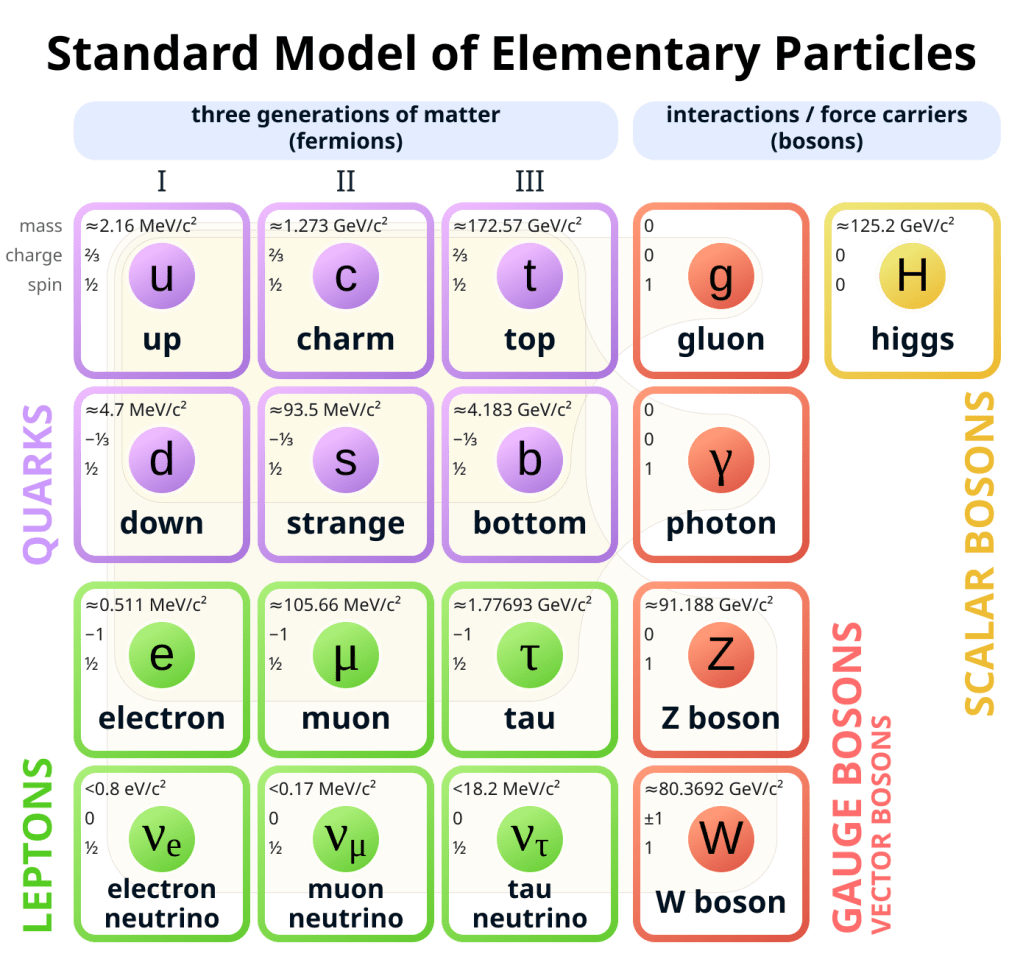
I’m glad it’s the end of the week. It’s been ridiculously busy. It didn’t help that I was already exhausted before it started, after a hectic three days in Geneva. Part of the reason for being so heavily occupied is that my teaching duties have just doubled. I teach the second half of a module called Nuclear and Particle Physics, and I’ve just taken over  for the second half of the semester to cover the part about particle physics. I started my set of 11 lectures with one about natural units, which is a lot of fun because it usually divides the class into two opposing camps.

About half the students think natural units are crazy, and the other half think they’re great. I’m in the second camp. The motivation is straightforward: particle physics combines quantum theory, which involves Planck’s constant

\hbar \simeq 1.05 \times 10^{-34}\,\,\,{\rm Js}

with special relativity, which involves the speed of light

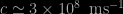c\simeq 3 \times 10^{8}\,\,\,{\rm m s}^{-1} .

Using everyday SI units (metres, seconds and kilograms) to deal with quantities that are either ridiculously small or ridiculously large doesn’t make any sense but, more importantly, the SI units don’t really reflect the physics very clearly.

In natural units we take these two constants to be equal to unity, so they don’t appear in any formulae:

\hbar = c =1

For example, the energy invariant in special relativity is usually written

E^2=p^2c^2 + m^2c^4

This is where the most famous equation in physics

E=mc^2

comes from. However, the equivalence between mass and energy (and also momentum) is much more clearly expressed in the natural units system:

E^2=p^2 + m^2

None of those tiresome factors of c^2 to remember! Mass, energy and momentum are all expressed in terms of the same natural unit of energy (usually, in particle physics, the GeV).  You can keep track of which is which by the simple expedient of using different names.

Velocities are, of course, always expressed as a fraction of c in this system so have no units.

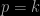In quantum theory we find energy E=\hbar \omega becomes E=\omega so energy is expressed in the same units as frequency. Energy is thus a measure of inverse time.  Momentum p =\hbar k becomes just p= k so momentum is an inverse length.  This is in accord with the various forms of Heisenberg’s Uncertainty Principle too:  \Delta p \Delta x \sim \hbar is \Delta p \Delta x \sim 1 and \Delta E \Delta t \sim \hbar becomes \Delta E \Delta t \sim 1. A particle with a finite lifetime thus has a finite energy width which is inversely proportional to the lifetime. It makes sense to use energy units for both of these things.

As an extra bonus we can dispense with the clumsy way that electromagnetism is handled in the SI system by noting that

\frac{e^2}{4\pi \epsilon_0 \hbar c} \equiv \alpha\simeq \frac{1}{137}

is dimensionless. In the SI system the coulomb force between two electrons is \frac{e^2}{4\pi \epsilon_0 r^2} whereas in natural units it is just \frac{\alpha}{r^2}, which is much nicer. Incidentally, the strange quantity \epsilon_0 that appears in the SI version is called the permittivity of free space. Nice name, but I wonder what it means?

The dimensionless quantity \alpha on the other hand, has a very clear  physical meaning: it is the fine structure constant,  a coupling constant that measures the strength of the electromagnetic interaction.

Some people – including emeritus professors of observational astronomy – object to natural units because they hide the units that things are expressed in. They don’t actually. What they do is express things in units that are better geared to the physics. In any case, if you want to convert back to SI units you can always do so straightforwardly with a little bit of dimensional analysis. This is necessary if you have to talk to engineers and the like, perhaps so they can build you a particle accelerator, but in the more elevated company of particle physicists you should definitely follow proper etiquette and keep your units natural.

22 Comments »