Archive for cosmological principle

« Older Entries

Timescape versus Dark Energy?

Posted in Astrohype, Open Access, The Universe and Stuff with tags , , , , , , , on January 2, 2025 by telescoper

Just before the Christmas break I noticed a considerable amount of press coverage claiming that Dark Energy doesn’t exist. Much of the media discussion is closely based on a press release produced by the Royal Astronomical Society. Despite the excessive hype, and consequent initial scepticism, I think the paper has some merit and raises some interesting issues.

The main focus of the discussion is a paper (available on arXiv here) by Seifert et al. with the title Supernovae evidence for foundational change to cosmological models. This paper is accompanied by a longer article called Cosmological foundations revisited with Pantheon+ (also available on arXiv) by a permutation of the same authors, which goes into more detail about the analysis of supernova observations. If you want some background, the “standard” Pantheon+ supernova analysis is described in this paper. The reanalysis presented in the recent papers is motivated an idea called the Timescape model, which is not new. It was discussed by David Wiltshire (one of the authors of the recent papers) in 2007 here and in a number of subsequent papers; there’s also a long review article by Wiltshire here (dated 2013).

So what’s all the fuss about?

Simulation of the Cosmic Web

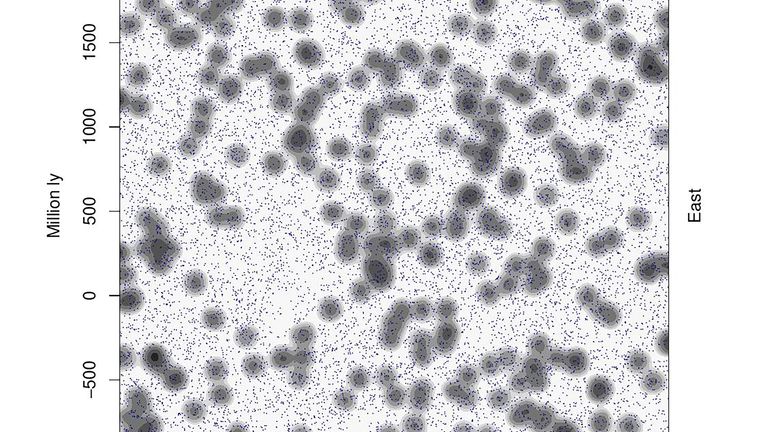
In the standard cosmological model we assume that, when sufficiently coarse-grained, the Universe obeys the Cosmological Principle, i.e. that it is homogeneous and isotropic. This implies that the space-time is described by a Friedmann–Lemaître–Robertson–Walker metric (FLRW) metric. Of course we know that the Universe is not exactly smooth. There is a complex cosmic web of galaxies, filaments, clusters, and giant voids which comprise the large-scale structure of the Universe. In the standard cosmological model these fluctuations are treated as small perturbations on a smooth background which evolve linearly on large scales and don’t have a significant effect on the global evolution of the Universe.

This standard model is very successful in accounting for many things but only at the expense of introducing dark energy whose origin is uncertain but which accounts for about 70% of the energy density of the Universe. Among other things, this accounts for the apparent acceleration of the Universe inferred from supernovae measurements.

The standard cosmology’s energy budget

The approach taken in the Timescape model is to dispense with the FLRW metric, and the idea of separating the global evolution from the inhomogeneities. The idea instead is that the cosmic structure is essentially non-linear so there is no “background metric”. In this model, cosmological observations can not be analysed within the standard framework which relies on the FLRW assumption. Hence the need to reanalyse the supernova data. The name Timescape refers to the presence of significant gravitational time-dilation effects in this model as distinct from the standard model.

I wrote before in the context of a different paper:

….the supernovae measurements do not directly measure cosmic acceleration. If one tries to account for them with a model based on Einstein’s general relativity and the assumption that the Universe is on large-scales is homogeneous and isotropic and with certain kinds of matter and energy then the observations do imply a universe that accelerates. Any or all of those assumptions may be violated (though some possibilities are quite heavily constrained). In short we could, at least in principle, simply be interpreting these measurements within the wrong framework…

So what to make of the latest papers? I have to admit that I didn’t follow all the steps of the supernova reanalysis. I hope an expert can comment on this! I will therefore restrict myself to some general comments.

  • My attitude to the standard cosmological model is that it is simply a working hypothesis and we should not elevate it to a status any higher than that. It is based not only on the Cosmological Principle (which could be false), but on the universal applicability of general relativity (which might not be true), and on a number of other assumptions that might not be true either.
  • It is important to recognize that one of the reasons that the standard cosmology is the front-runner is that it provides a framework that enables relatively straightforward prediction and interpretation of cosmological measurements. That goes not only for supernova measurements but also for the cosmic microwave background, galaxy clustering, gravitational lensing, and so on. This is much harder to do accurately in the Timescape model simply because the equations involved are much more complex; there are few exact solutions of Einstein’s equations that can help. It is important that people work on alternatives such as this.
  • Second, the idea that inhomogeneities might be much more important than assumed in the standard model has been discussed extensively in the literature over the last twenty years or so under the heading “backreaction”. My interpretation of the current state of play is that there are many unresolved questions, largely because of technical difficulties. See, for example, work by Thomas Buchert (here and, with many other collaborators here) and papers by Green & Wald (here and here). Nick Kasiser also wrote about it here.
  • The new papers under discussion focus entirely on supernovae measurements. It must be recognized that these provide just one of the pillars supporting the standard cosmology. Over the years, many alternative models have been suggested that claim to “fix” some alleged problem with cosmology only to find that it makes other issues worse. That’s not a reason to ignore departures from the standard framework, but it is an indication that we have a huge amount of data and we’re not allowed to cherry-pick what we want. We have to fit it all. The strongest evidence in favour of the FLRW framework actually comes from the cosmic microwave background (CMB) with the supernovae provide corroboration. I would need to see a detailed prediction of the anisotropy of the CMB before being convinced.
  • The Timescape model is largely based on the non-linear expansion of cosmic voids. These are undoubtedly important, and there has been considerable observational and theoretical activity in understanding them and their evolution in the standard model. It is not at all obvious to me that the voids invoked to explain the apparent acceleration of the Universe are consistent with what we actually see in our surveys. That is something else to test.
  • Finally, the standard cosmology includes a prescription for the initial conditions from which the present inhomogeneities grew. Where does the cosmic web come from in the Timescape model?

Anyway, I’m sure there’ll be a lot of discussion of this in the next few weeks as cosmologists return to the Universe from their Christmas holidays!

Comments are welcome through the box below, especially from people who have managed to understand the cos.

9 Comments »

The Big Ring Circus

Posted in Astrohype, Bad Statistics, The Universe and Stuff with tags , , , , on January 15, 2024 by telescoper

At the annual AAS Meeting in New Orleans last week there was an announcement of a result that made headlines in the media (see, e.g., here and here). There is also a press release from the University of Central Lancashire.

Here is a video of the press conference:

I was busy last week so didn’t have time to read the details so refrained from commenting on this issue at the time of the announcement. Now that I am back in circulation, I have time to read the details, but unfortunately was unable to find even a preprint describing this “discovery”. The press conference doesn’t contain much detail either so it’s impossible to say anything much about the significance of the result, which is claimed (without explanation) to be 5.2σ (after “doing some statistics”). I see the “Big Ring” now has its own wikipedia page, the only references on which are to press reports, not peer-reviewed scientific papers or even preprints.

So is this structure “so big it challenges our understanding of the universe”?

The Big Ring (blue) and another large structure (red)
Spot the Ring in the actual data

Based on the available information it is impossible to say. The large-scale structure of the Universe comprises a complex network of walls and filaments known as the cosmic web which I have written about numerous times on this blog. This structure is so vast and complicated that it is very easy to find strange shapes in it but very hard to determine whether or not they indicate anything other than an over-active imagination.

To assess the significance of the Big Ring or other structures in a proper scientific fashion, one has to calculate how probable that structure is given a model. We have a standard model that can be used for this purpose, but to simulate very structures is not straightforward because it requires a lot of computing power even to simulate just the mass distribution. In this case one also has to understand how to embed Magnesium absorption too, something which may turn out to trace the mass in a very biased way. Moreover, one has to simulate the observational selection process too, so one is doing a fair comparison between observations and predictions.

I have seen no evidence that this has been done in this case. When it is, I’ll comment on the details. I’m not optimistic however, as the description given in the media accounts contains numerous falsehoods. For example, quoting the lead author:

The Cosmological Principle assumes that the part of the universe we can see is viewed as a ‘fair sample’ of what we expect the rest of the universe to be like. We expect matter to be evenly distributed everywhere in space when we view the universe on a large scale, so there should be no noticeable irregularities above a certain size.

https://www.uclan.ac.uk/news/big-ring-in-the-sky

This just isn’t correct. The standard cosmology has fluctuations on all scales. Although the fluctuation amplitude decreases with scale, there is no scale at which the Universe is completely smooth. See the discussion, for example, here. We can see correlations on very large angular scales in the cosmic microwave background which would be absent if the Universe were completely smooth on those scales. The observed structure is about 400 Mpc in size, which does not seem to be to be particularly impressive.

I suspect that the 5.2σ figure mentioned above comes from some sort of comparison between the observed structure and a completely uniform background, in which case it is meaningless.

My main comment on this episode is that I think it’s very poor practice to go hunting headlines when there isn’t even a preprint describing the results. That’s not the sort of thing PhD supervisors should be allowing their PhD students to do. As I have mentioned before on this blog, there is an increasing tendency for university press offices to see themselves entirely as marketing agencies instead of informing and/or educating the public. Press releases about scientific research nowadays rarely make any attempt at accuracy – they are just designed to get the institution concerned into the headlines. In other words, research is just a marketing tool.

In the long run, this kind of media circus, driven by hype rather than science, does nobody any good.

P.S. I was going to joke that ring-like structures can be easily explained by circular reasoning, but decided not to.

12 Comments »

Debating the Cosmological Principle

Posted in The Universe and Stuff with tags , , , , on November 5, 2020 by telescoper

Whether you need something to distract you from world events or are just interested in the subject I thought I’d share something cosmological today.

You may recall that I recently posted about a paper by Subir Sarkar and collaborators.  Here is the abstract and author list:

In that post I mentioned that Subir would be taking part in an online debate about this issue. Well, although I wasn’t able to watch it live there is a recording of it which is available here:

It’s rather long, but there are many interesting things in it…

Leave a comment »

A Test of the Cosmological Principle using Quasars

Posted in The Universe and Stuff with tags , , , , on October 8, 2020 by telescoper

I’m not getting much time these days to even think about cosmology but Subir Sarkar drew my attention to an intriguing paper by his team so I thought I’d share it here. Here is the abstract and author list:

I find this an intriguing result because I’ve often wondered about the dipole anisotropy of the cosmic microwave background might not be exclusively kinematic in origin and whether they might also be a primordial contribution. The dipole (180°) variation corresponds to a ΔT/T of order 10-3, which a hundred times larger than the variation on any other angular scale. This is what it looks like:

This is usually interpreted as being due to the motion of the observer through a frame in which the cosmic microwave background is completely isotropic. A simple calculation then gives the speed of this motion using ΔT/T ≈ v/c. This motion is assumed to be generated by gravitational interaction with local density fluctuations rather than being due to anything truly cosmological (i.e. of primordial origin).

The features in the cosmic microwave background temperature pattern on smaller angular scales (the quadrupole, octopole, etc…) , which have ΔT/T of order 10-5 are different in that they are dominated by primordial density fluctuations. There should be a primordial dipole at some level, but the fact that these other harmonic modes have such low amplitudes and the assumption that the primordial dipole should be of the same order, combined with the fact that the CMB dipole does indeed roughly line up with the dipole expected to be generated by local inhomogeneities, has led to the widespread belief that this intrinsic dipole is negligible. This analysis suggests that it might not be.

What the authors have done is study the anisotropy of a large sample of quasars (going out to redshifts of order three) finding the dipole to be larger than that of the CMB. Note however that the sample does not cover the whole sky because of a mask to remove regions wherein AGN are hard to observe:

As well as the mask there are other possible systematics that might be at play, which I am sure will be interrogated when the paper is peer-reviewed which, as far as I know, is not yet the case.

P.S. I might just quibble a little bit about the last sentence of the abstract. We know that the Universe violates the cosmological principle even in the standard model: with scale-invariant perturbations there is no scale at which the Universe is completely homogeneous. The question is really how much and in what way it is violated. We seem to be happy with 10-5 but not with 10-3…

Update: On 23rd October Subir will be giving a talk about this an participating in a debate. For more details, see here.

6 Comments »

Gamma-Ray Bursts and the Cosmological Principle

Posted in Astrohype, Bad Statistics, The Universe and Stuff with tags , , , on September 13, 2015 by telescoper

There’s been a reasonable degree of hype surrounding a paper published in Monthly Notices of the Royal Astronomical Society (and available on the arXiv here). The abstract of this paper reads:

According to the cosmological principle (CP), Universal large-scale structure is homogeneous and isotropic. The observable Universe, however, shows complex structures even on very large scales. The recent discoveries of structures significantly exceeding the transition scale of 370 Mpc pose a challenge to the CP. We report here the discovery of the largest regular formation in the observable Universe; a ring with a diameter of 1720 Mpc, displayed by 9 gamma-ray bursts (GRBs), exceeding by a factor of 5 the transition scale to the homogeneous and isotropic distribution. The ring has a major diameter of 43° and a minor diameter of 30° at a distance of 2770 Mpc in the 0.78 < z < 0.86 redshift range, with a probability of 2 × 10−6 of being the result of a random fluctuation in the GRB count rate. Evidence suggests that this feature is the projection of a shell on to the plane of the sky. Voids and string-like formations are common outcomes of large-scale structure. However, these structures have maximum sizes of 150 Mpc, which are an order of magnitude smaller than the observed GRB ring diameter. Evidence in support of the shell interpretation requires that temporal information of the transient GRBs be included in the analysis. This ring-shaped feature is large enough to contradict the CP. The physical mechanism responsible for causing it is unknown.

The so-called “ring” can be seen here:
ring_Australia

In my opinion it’s not a ring at all, but an outline of Australia. What’s the probability of a random distribution of dots looking exactly like that? Is it really evidence for the violation of the Cosmological Principle, or for the existence of the Cosmic Antipodes?

For those of you who don’t get that gag, a cosmic antipode occurs in, e.g., closed Friedmann cosmologies in which the spatial sections take the form of a hypersphere (or 3-sphere). The antipode is the point diametrically opposite the observer on this hypersurface, just as it is for the surface of a 2-sphere such as the Earth. The antipode is only visible if it lies inside the observer’s horizon, a possibility which is ruled out for standard cosmologies by current observations. I’ll get my coat.

Anyway, joking apart, the claims in the abstract of the paper are extremely strong but the statistical arguments supporting them are deeply unconvincing. Indeed, I am quite surprised the paper passed peer review. For a start there’s a basic problem of “a posteriori” reasoning here. We see a group of objects that form a map of Australia ring and then are surprised that such a structure appears so rarely in simulations of our favourite model. But all specific configurations of points are rare in a Poisson point process. We would be surprised to see a group of dots in the shape of a pretzel too, or the face of Jesus, but that doesn’t mean that such an occurrence has any significance. It’s an extraordinarily difficult problem to put a meaningful measure on the space of geometrical configurations, and this paper doesn’t succeed in doing that.

For a further discussion of the tendency that people have to see patterns where none exist, take a look at this old post from which I’ve taken this figure which is generated by drawing points independently and uniformly randomly:

pointaI can see all kinds of shapes in this pattern, but none of them has any significance (other than psychological). In a mathematically well-defined sense there is no structure in this pattern! Add to that difficulty the fact that so few points are involved and I think it becomes very clear that this “structure” doesn’t provide any evidence at all for the violation of the Cosmological Principle. Indeed it seems neither do the authors. The very last paragraph of the paper is as follows:

GRBs are very rare events superimposed on the cosmic
web identified by superclusters. Because of this, the ring is
probably not a real physical structure. Further studies are
needed to reveal whether or not the Ring could have been
produced by a low-frequency spatial harmonic of the large-
scale matter density distribution and/or of universal star
forming activity.

It’s a pity that this note of realism didn’t make it into either the abstract or, more importantly, the accompanying press release. Peer review will never be perfect, but we can do without this sort of hype. Anyway, I confidently predict that a proper refutation will appear shortly….

P.S. For a more technical discussion of the problems of inferring the presence of large structures from sparsely-sampled distributions, see here.

16 Comments »

The Fractal Universe, Part 2

Posted in History, The Universe and Stuff with tags , , , , , , on June 27, 2014 by telescoper

Given the recent discussion in comments on this blog I thought I’d give a brief update on the issue of the scale of cosmic homogeneity; I’m going to repeat some of the things I said in a post earlier this week just to make sure that this discussion is reasonable self-contained.

Our standard cosmological model is based on the Cosmological Principle, which asserts that the Universe is, in a broad-brush sense, homogeneous (is the same in every place) and isotropic (looks the same in all directions). But the question that has troubled cosmologists for many years is what is meant by large scales? How broad does the broad brush have to be? A couple of presentations discussed the possibly worrying evidence for the presence of a local void, a large underdensity on scale of about 200 MPc which may influence our interpretation of cosmological results.

I blogged some time ago about that the idea that the Universe might have structure on all scales, as would be the case if it were described in terms of a fractal set characterized by a fractal dimension D. In a fractal set, the mean number of neighbours of a given galaxy within a spherical volume of radius R is proportional to R^D. If galaxies are distributed uniformly (homogeneously) then D = 3, as the number of neighbours simply depends on the volume of the sphere, i.e. as R^3, and the average number-density of galaxies. A value of D < 3 indicates that the galaxies do not fill space in a homogeneous fashion: D = 1, for example, would indicate that galaxies were distributed in roughly linear structures (filaments); the mass of material distributed along a filament enclosed within a sphere grows linear with the radius of the sphere, i.e. as R^1, not as its volume; galaxies distributed in sheets would have D=2, and so on.

We know that D \simeq 1.2 on small scales (in cosmological terms, still several Megaparsecs), but the evidence for a turnover to D=3 has not been so strong, at least not until recently. It’s just just that measuring D from a survey is actually rather tricky, but also that when we cosmologists adopt the Cosmological Principle we apply it not to the distribution of galaxies in space, but to space itself. We assume that space is homogeneous so that its geometry can be described by the Friedmann-Lemaitre-Robertson-Walker metric.

According to Einstein’s theory of general relativity, clumps in the matter distribution would cause distortions in the metric which are roughly related to fluctuations in the Newtonian gravitational potential \delta\Phi by \delta\Phi/c^2 \sim \left(\lambda/ct \right)^{2} \left(\delta \rho/\rho\right), give or take a factor of a few, so that a large fluctuation in the density of matter wouldn’t necessarily cause a large fluctuation of the metric unless it were on a scale \lambda reasonably large relative to the cosmological horizon \sim ct. Galaxies correspond to a large \delta \rho/\rho \sim 10^6 but don’t violate the Cosmological Principle because they are too small in scale \lambda to perturb the background metric significantly.

In my previous post I left the story as it stood about 15 years ago, and there have been numerous developments since then, some convincing (to me) and some not. Here I’ll just give a couple of key results, which I think to be important because they address a specific quantifiable question rather than relying on qualitative and subjective interpretations.

The first, which is from a paper I wrote with my (then) PhD student Jun Pan, demonstrated what I think is the first convincing demonstration that the correlation dimension of galaxies in the IRAS PSCz survey does turn over to the homogeneous value D=3 on large scales:

correlations

You can see quite clearly that there is a gradual transition to homogeneity beyond about 10 Mpc, and this transition is certainly complete before 100 Mpc. The PSCz survey comprises “only” about 11,000 galaxies, and it relatively shallow too (with a depth of about 150 Mpc),  but has an enormous advantage in that it covers virtually the whole sky. This is important because it means that the survey geometry does not have a significant effect on the results. This is important because it does not assume homogeneity at the start. In a traditional correlation function analysis the number of pairs of galaxies with a given separation is compared with a random distribution with the same mean number of galaxies per unit volume. The mean density however has to be estimated from the same survey as the correlation function is being calculated from, and if there is large-scale clustering beyond the size of the survey this estimate will not be a fair estimate of the global value. Such analyses therefore assume what they set out to prove. Ours does not beg the question in this way.

The PSCz survey is relatively sparse but more recently much bigger surveys involving optically selected galaxies have confirmed this idea with great precision. A particular important recent result came from the WiggleZ survey (in a paper by Scrimgeour et al. 2012). This survey is big enough to look at the correlation dimension not just locally (as we did with PSCz) but as a function of redshift, so we can see how it evolves. In fact the survey contains about 200,000 galaxies in a volume of about a cubic Gigaparsec. Here are the crucial graphs:

homogeneity

I think this proves beyond any reasonable doubt that there is a transition to homogeneity at about 80 Mpc, well within the survey volume. My conclusion from this and other studies is that the structure is roughly self-similar on small scales, but this scaling gradually dissolves into homogeneity. In a Fractal Universe the correlation dimension would not depend on scale, so what I’m saying is that we do not live in a fractal Universe. End of story.

16 Comments »

The Zel’dovich Universe – Day 4 Summary

Posted in History, The Universe and Stuff with tags , , , , , , , on June 27, 2014 by telescoper

And on the fourth day of this meeting about “The Zel’dovich Universe”  we were back to a full schedule (9am until 7.30pm) concentrating on further studies of the Cosmic Web. We started off with a discussion of the properties of large-scale structure at high redshift. As someone who’s old enough to remember the days when “high redshift” meant about z~0.1 the idea that we can now map the galaxy distribution at redshifts z~2. There are other measures of structure on these huge scales, such as the Lyman alpha forest, and we heard a bit about some of them too.

The second session was about “reconstructing” the Cosmic Web, although a more correct word have been “deconstructing”. The point about this session is that cosmology is basically a backwards subject. In other branches of experimental science we set the initial conditions for a system and then examine how it evolves. In cosmology we have to infer the initial conditions of the Universe from what we observe around us now. In other words, cosmology is an inverse problem on a grand scale.  In the context of the cosmic web, we want to infer the pattern of initial density and velocity fluctuations that gave rise to the present network of clusters, filaments and voids. Several talks about this emphasized how proper Bayesian methods have led to enormous progress in this field over the last few years.

All this progress has been accompanied by huge improvements in graphical visualisation techniques. Thirty years ago the state of the art in this field was represented by simple contour plots, such as this (usually called the Cosmic Chicken):

chicken

You can see how crude this representation is by comparing it with a similar plot from the modern era of precision cosmology:

chicken

Even better examples are provided by the following snapshot:

IMG-20140626-00352

It’s nice to see a better, though still imperfect,  version of the chicken at the top right, though I found the graphic at the bottom right rather implausible; it must be difficult to skate at all with those things around your legs.

Here’s another picture I liked, despite the lack of chickens:

IMG-20140626-00353

Incidentally, it’s the back of Alar Toomre‘s head you can see on the far right in this picture.

The afternoon was largely devoted to discussions of how the properties of individual galaxies are influenced by their local environment within the Cosmic Web. I usually think of galaxies as test particles (i.e. point masses) but they are interesting in their own right (to some people anyway). However, the World Cup intervened during the evening session and I skipped a couple of talks to watch Germany beat the USA in their final group match.

That’s all for now. Tonight we’ll have the conference dinner, which is apparently being held in the “House of Blackheads” on “Pikk Street”. Sounds like an interesting spot!

Leave a comment »

The Zel’dovich Universe – Day 3 Summary

Posted in History, The Universe and Stuff with tags , , , , , , on June 26, 2014 by telescoper

Day Three of this meeting about “The Zel’dovich Universe” was slightly shorter than the previous two, in that it finished just after 17.00 rather than the usual 19.00 or later. That meant that we got out in time to settle down for a beer in time the World Cup football. I watched an excellent game between Nigeria and Argentina, which ended 3-2 to Argentina but could have been 7-7. I’ll use that as an excuse for writing a slightly shorter summary.

Anyway we began with a session on the Primordial Universe and Primordial Signatures led off by Alexei Starobinsky (although there is some controversy whether his name should end -y or -i). Starobinsky outlined the theory of cosmological perturbations from inflation with an emphasis on how it relates to some of Zel’dovich’s ideas on the subject. There was then a talk from Bruce Partridge about some of the results from Planck. I’ve mentioned already that this isn’t a typical cosmology conference, and this talk provided another unusual aspect in that there’s hardly been any discussion of the BICEP2 results here. When asked about at the end of his talk, Bruce replied (very sensibly) that we should all just be patient.

Next session after coffee was about cosmic voids, kicked off by Rien van de Weygaert with a talk entitled “Much Ado About Nothing”, which reminded me of the following quote from the play of the same name:

“He hath indeed better bettered expectation than you must expect of me to tell you how”

The existence of voids in the galaxy distribution is not unexpected given the presence of clusters and superclusters, but they are interesting in their own right as they display particular dynamical evolution and have important consequences on observations. In 1984, Vincent Icke proved the so-called “Bubble Theorem” which showed that an isolated underdensity tends to evolve to a spherical shape.Most cosmologists, including myself, therefore expected big voids to be round, which turns out to be wrong; the interaction of the perimeter of the void with its surroundings always plays an important role in determining the geometry. Another thing that sprang into my mind was a classic paper by Simon White (1979) with the abstract:

We derive and display relations which can be used to express many quantitative measures of clustering in terms of the hierarchy of correlation functions. The convergence rate and asymptotic behaviour of the integral series which usually result is explored as far as possible using the observed low-order galaxy correlation functions. On scales less than the expected nearest neighbour distance most clustering measures are influenced only by the lowest order correlation functions. On all larger scales their behaviour, in general, depends significantly on correlations of high order and cannot be approximated using the low-order functions. Bhavsar’s observed relation between density enhancement and the fraction of galaxies included in clusters is modelled and is shown to be only weakly dependent on high-order correlations over most of its range. The probability that a randomly placed region of given volume be empty is discussed as a particularly simple and appealing example of a statistic which is strongly influenced by correlations of all orders, and it is shown that this probability may obey a scaling law which will allow a test of the small-scale form of high-order correlations.

The emphasis is mine. It’s fascinating and somewhat paradoxical that we can learn a lot about the statistics of where the galaxies are fom the regions where galaxies are not.

Another thing worth mentioning was Paul Sutter’s discussion of a project on cosmic voids which is a fine example of open science. Check out the CosmicVoids website where you will find void catalogues, identification algorithms and a host of other stuff all freely available to anyone who wants to use them. This is the way forward.

After lunch we had a session on Cosmic Flows, with a variety of talks about using galaxy peculiar velocities to understand the dynamics of large-scale structure. This field was booming about twenty years ago but which has been to some extent been overtaken by other cosmological probes that offer greater precision; the biggest difficulty has been getting a sufficient number of sufficiently accurate direct (redshift-independent) distance measurements to do good statistics. It remains a difficult but important field, because it’s important to test our models with as many independent methods as possible.

I’ll end with a word about the first speaker of this session, the Gruber prize winner Marc Davis. He suffered a stroke a few years ago which has left him partly paralysed (down his right side). He has battled back from this with great courage, and even turned it to his advantage during his talk when he complained about how faint the laser pointer was and used his walking stick instead.

IMG-20140625-00351

2 Comments »

The Zel’dovich Universe – Day 2 Summary

Posted in History, The Universe and Stuff with tags , , , on June 25, 2014 by telescoper

IMG-20140624-00349

Day Two of this enjoyable meeting involved more talks about the cosmic web of large-scale structure of the Universe. I’m not going to attempt to summarize the whole day, but will just mention a couple of things that made me reflect a bit. Unfortunately that means I won’t be able to do more than merely mention some of the other fascinating things that came up, as phase-space flip-flops and one-dimensional Origami.

One was a very nice review by John Peacock in which he showed that a version of Moore’s law applies to galaxy redshift surveys; since the first measurement of the redshift of an extragalactic object by Slipher in 1912, the number of redshifts has doubled every 2-3 years ago. This exponential growth has been driven by improvements in technology, from photographic plates to electronic detectors and from single-object spectroscopy to multiplex technology and so on. At this rate by 2050 or so we should have redshifts for most galaxies in the observable Universe. Progress in cosmography has been remarkable indeed.

The term “Cosmic Web” may be a bit of a misnomer in fact, as a consensus may be emerging that in some sense it is more like a honeycomb. Thanks to a miracle of 3D printing, here is an example of what the large-scale structure of the Universe seems to look like:

IMG-20140624-00350

One of the issues that emerged from the mix of theoretical and observational talks concerned the scale of cosmic homogeneity. Our standard cosmological model is based on the Cosmological Principle, which asserts that the Universe is, in a broad-brush sense, homogeneous (is the same in every place) and isotropic (looks the same in all directions). But the question that has troubled cosmologists for many years is what is meant by large scales? How broad does the broad brush have to be? A couple of presentations discussed the possibly worrying evidence for the presence of a local void, a large underdensity on scale of about 200 MPc which may influence our interpretation of cosmological results.

I blogged some time ago about that the idea that the Universe might have structure on all scales, as would be the case if it were described in terms of a fractal set characterized by a fractal dimension D. In a fractal set, the mean number of neighbours of a given galaxy within a spherical volume of radius R is proportional to R^D. If galaxies are distributed uniformly (homogeneously) then D = 3, as the number of neighbours simply depends on the volume of the sphere, i.e. as R^3, and the average number-density of galaxies. A value of D < 3 indicates that the galaxies do not fill space in a homogeneous fashion: D = 1, for example, would indicate that galaxies were distributed in roughly linear structures (filaments); the mass of material distributed along a filament enclosed within a sphere grows linear with the radius of the sphere, i.e. as R^1, not as its volume; galaxies distributed in sheets would have D=2, and so on.

We know that D \simeq 1.2 on small scales (in cosmological terms, still several Megaparsecs), but the evidence for a turnover to D=3 has not been so strong, at least not until recently. It’s just just that measuring D from a survey is actually rather tricky, but also that when we cosmologists adopt the Cosmological Principle we apply it not to the distribution of galaxies in space, but to space itself. We assume that space is homogeneous so that its geometry can be described by the Friedmann-Lemaitre-Robertson-Walker metric.

According to Einstein’s theory of general relativity, clumps in the matter distribution would cause distortions in the metric which are roughly related to fluctuations in the Newtonian gravitational potential \delta\Phi by \delta\Phi/c^2 \sim \left(\lambda/ct \right)^{2} \left(\delta \rho/\rho\right), give or take a factor of a few, so that a large fluctuation in the density of matter wouldn’t necessarily cause a large fluctuation of the metric unless it were on a scale \lambda reasonably large relative to the cosmological horizon \sim ct. Galaxies correspond to a large \delta \rho/\rho \sim 10^6 but don’t violate the Cosmological Principle because they are too small in scale \lambda to perturb the background metric significantly.

The discussion of a fractal universe is one I’m overdue to return to. In my previous post I left the story as it stood about 15 years ago, and there have been numerous developments since then, not all of them consistent with each other. I will do a full “Part 2” to that post eventually, but in the mean time I’ll just comment that current large surveys, such as those derived from the Sloan Digital Sky Survey, do seem to be consistent with a Universe that possesses the property of large-scale homogeneity. If that conclusion survives the next generation of even larger galaxy redshift surveys then it will come as an immense relief to cosmologists.

The reason for that is that the equations of general relativity are very hard to solve in cases where there isn’t a lot of symmetry; there are just too many equations to solve for a general solution to be obtained. If the cosmological principle applies, however, the equations simplify enormously (both in number and form) and we can get results we can work with on the back of an envelope. Small fluctuations about the smooth background solution can be handled (approximately but robustly) using a technique called perturbation theory. If the fluctuations are large, however, these methods don’t work. What we need to do instead is construct exact inhomogeneous model, and that is very very hard. It’s of course a different question as to why the Universe is so smooth on large scales, but as a working cosmologist the real importance of it being that way is that it makes our job so much easier than it would otherwise be.

PS. If anyone reading this either at the conference or elsewhere has any questions or issues they would like me to raise during the summary talk on Saturday please don’t hesitate to leave a comment below or via Twitter using the hashtag .

30 Comments »

The Importance of Being Homogeneous

Posted in The Universe and Stuff with tags , , , , , , , , on August 29, 2012 by telescoper

A recent article in New Scientist reminded me that I never completed the story I started with a couple of earlier posts (here and there), so while I wait for the rain to stop I thought I’d make myself useful by posting something now. It’s all about a paper available on the arXiv by Scrimgeour et al. concerning the transition to homogeneity of galaxy clustering in the WiggleZ galaxy survey, the abstract of which reads:

We have made the largest-volume measurement to date of the transition to large-scale homogeneity in the distribution of galaxies. We use the WiggleZ survey, a spectroscopic survey of over 200,000 blue galaxies in a cosmic volume of ~1 (Gpc/h)^3. A new method of defining the ‘homogeneity scale’ is presented, which is more robust than methods previously used in the literature, and which can be easily compared between different surveys. Due to the large cosmic depth of WiggleZ (up to z=1) we are able to make the first measurement of the transition to homogeneity over a range of cosmic epochs. The mean number of galaxies N(<r) in spheres of comoving radius r is proportional to r^3 within 1%, or equivalently the fractal dimension of the sample is within 1% of D_2=3, at radii larger than 71 \pm 8 Mpc/h at z~0.2, 70 \pm 5 Mpc/h at z~0.4, 81 \pm 5 Mpc/h at z~0.6, and 75 \pm 4 Mpc/h at z~0.8. We demonstrate the robustness of our results against selection function effects, using a LCDM N-body simulation and a suite of inhomogeneous fractal distributions. The results are in excellent agreement with both the LCDM N-body simulation and an analytical LCDM prediction. We can exclude a fractal distribution with fractal dimension below D_2=2.97 on scales from ~80 Mpc/h up to the largest scales probed by our measurement, ~300 Mpc/h, at 99.99% confidence.

To paraphrase, the conclusion of this study is that while galaxies are strongly clustered on small scales – in a complex `cosmic web’ of clumps, knots, sheets and filaments –  on sufficiently large scales, the Universe appears to be smooth. This is much like a bowl of porridge which contains many lumps, but (usually) none as large as the bowl it’s put in.

Our standard cosmological model is based on the Cosmological Principle, which asserts that the Universe is, in a broad-brush sense, homogeneous (is the same in every place) and isotropic (looks the same in all directions). But the question that has troubled cosmologists for many years is what is meant by large scales? How broad does the broad brush have to be?

I blogged some time ago about that the idea that the  Universe might have structure on all scales, as would be the case if it were described in terms of a fractal set characterized by a fractal dimension D. In a fractal set, the mean number of neighbours of a given galaxy within a spherical volume of radius R is proportional to R^D. If galaxies are distributed uniformly (homogeneously) then D = 3, as the number of neighbours simply depends on the volume of the sphere, i.e. as R^3, and the average number-density of galaxies. A value of D < 3 indicates that the galaxies do not fill space in a homogeneous fashion: D = 1, for example, would indicate that galaxies were distributed in roughly linear structures (filaments); the mass of material distributed along a filament enclosed within a sphere grows linear with the radius of the sphere, i.e. as R^1, not as its volume; galaxies distributed in sheets would have D=2, and so on.

We know that D \simeq 1.2 on small scales (in cosmological terms, still several Megaparsecs), but the evidence for a turnover to D=3 has not been so strong, at least not until recently. It’s just just that measuring D from a survey is actually rather tricky, but also that when we cosmologists adopt the Cosmological Principle we apply it not to the distribution of galaxies in space, but to space itself. We assume that space is homogeneous so that its geometry can be described by the Friedmann-Lemaitre-Robertson-Walker metric.

According to Einstein’s  theory of general relativity, clumps in the matter distribution would cause distortions in the metric which are roughly related to fluctuations in the Newtonian gravitational potential \delta\Phi by \delta\Phi/c^2 \sim \left(\lambda/ct \right)^{2} \left(\delta \rho/\rho\right), give or take a factor of a few, so that a large fluctuation in the density of matter wouldn’t necessarily cause a large fluctuation of the metric unless it were on a scale \lambda reasonably large relative to the cosmological horizon \sim ct. Galaxies correspond to a large \delta \rho/\rho \sim 10^6 but don’t violate the Cosmological Principle because they are too small in scale \lambda to perturb the background metric significantly.

The discussion of a fractal universe is one I’m overdue to return to. In my previous post  I left the story as it stood about 15 years ago, and there have been numerous developments since then, not all of them consistent with each other. I will do a full “Part 2” to that post eventually, but in the mean time I’ll just comment that this particularly one does seem to be consistent with a Universe that possesses the property of large-scale homogeneity. If that conclusion survives the next generation of even larger galaxy redshift surveys then it will come as an immense relief to cosmologists.

The reason for that is that the equations of general relativity are very hard to solve in cases where there isn’t a lot of symmetry; there are just too many equations to solve for a general solution to be obtained.  If the cosmological principle applies, however, the equations simplify enormously (both in number and form) and we can get results we can work with on the back of an envelope. Small fluctuations about the smooth background solution can be handled (approximately but robustly) using a technique called perturbation theory. If the fluctuations are large, however, these methods don’t work. What we need to do instead is construct exact inhomogeneous model, and that is very very hard. It’s of course a different question as to why the Universe is so smooth on large scales, but as a working cosmologist the real importance of it being that way is that it makes our job so much easier than it would otherwise be.

P.S. And I might add that the importance of the Scrimgeour et al paper to me personally is greatly amplified by the fact that it cites a number of my own articles on this theme!

2 Comments »

« Older Entries