Archive for general relativity

« Older Entries
Newer Entries »

Why is General Relativity so difficult?

Posted in The Universe and Stuff with tags , , on November 26, 2015 by telescoper

Just a brief post following yesterday’s centenary of General Relativity, after which somebody asked me what is so difficult about the theory. I had two answers to that, one mathematical and one conceptual.

einstein-equation1

The Field Equations of General Relativity are written above. In the notation used they don’t look all that scary, but they are more complicated than they look. For a start it looks like there is only one equation, but the subscripts μ and ν can each take four values (usually 0, 1, 2 or 3), each value standing for one of the dimensions of four-dimensional space time. It therefore looks likes there are actually 16 equations. However, the equations are the same if you swap μ  and ν around. This means that there are “only” ten independent equations. The terms on the left hand side are the components of the Einstein Tensor which expresses the effect of gravity through the curvature of space time and the right hand side describes the energy and momentum of “stuff”, prefaced by some familiar constants.

The Einstein Tensor is made up of lots of partial derivatives of another tensor called the metric tensor (which describes the geometry of space time), which relates, through the Field Equations, to how matter and energy are distributed and how these components move and interact. The ten equations that need to be solved simultaneously are second-order non-linear partial different equations. This is to be compared with the case of Newtonian gravity in which only ordinary different equations are involved.

Problems in Newtonian mechanics can be difficult enough to solve but the much greater mathematical complexity in General Relativity means that problems in GR can only be solved in cases of very special symmetry, in which the number of independent equations can be reduced dramatically.

So that’s why it’s difficult mathematically. As for the conceptual problem it’s that most people (I think) consider “space” to be “what’s in between the matter” which seems like it must be “nothing”. But how can “nothing” possess an attribute like curvature? This leads you to conclude that space is much more than nothing. But it’s not a form of matter. So what is it? This chain of thought often leads people to think of space as being like the Ether, but that’s not right either. Hmm.

I tend to avoid this problem by not trying to think about space or space-time at all, and instead think only in terms of particle trajectories or ligh rays and how matter and energy affect them. But that’s because I’m lazy and only have a small brain…

 

 

17 Comments »

100 Years of General Relativity

Posted in History, The Universe and Stuff with tags , on November 25, 2015 by telescoper

Many people have been celebrating the centenary of the birth of Einstein’s Theory of General Relativity this year, but it’s not obvious precisely what date to select. I’ve decided to go for today, partly because the News on BBC Radio 3 did when I work up this morning, but also because there is a well-known publication that mentions that date:

einsteingr

The 25th November 1915 was the date on which Einstein presented the “final” form of his theory to the Prussian Academy of Sciences. You can find a full translation of the paper “The Field Equations of Gravitation” here. You will see that he refers to a couple of earlier papers in that work, but I think this one is the first presentation of the full theory. It fascinated me when I was looking at the history of GR for the textbook I was working on about 20 years ago that the main results (e.g. on cosmology, the bending of light and on the perihelion of mercury) are spread over a large number of rather short papers rather than all being in one big one. I guess that was the style of the times!

So there you are, General Relativity has been around for 100 years. At least according to one particular reference frame…

 

Oh, and here’s a cute little video – funded by the Science and Technology Facilities Council – celebrating the centenary:

 

13 Comments »

My talk at “The Origins of the Expanding Universe”

Posted in Books, Talks and Reviews, The Universe and Stuff with tags , , , , , , on October 9, 2012 by telescoper

You may recall that I gave a talk recently at a meeting called The Origins of the Expanding Universe in Flagstaff, Arizona. I put the slides up here. Well, the organizers have now put videos of the presentations online so you have the chance to see mine, warts and all.

I was relieved when I saw this on Youtube that the organizers were kind enough to edit out the embarrassing bit at the start when my laptop refused to talk to the data projector and I had to swap to another one. Sorting all that out seemed to take ages, which didn’t help my frame of mind and I was even more nervous than I would have been anyway given that this was my first public appearance after a rather difficult summer. Those are my excuses for what was, frankly, not a particularly good talk. But at least I survived. Better is the end of a thing than the beginning thereof.

12 Comments »

Origins of the Expanding Universe Conference – My Contribution

Posted in History, The Universe and Stuff with tags , , , , , on September 19, 2012 by telescoper

For those of you interested in such things, here are the slides I used in my talk at the Origins of the Expanding Universe conference. I spoke about the events on and after 29th May 1919, when measurements were made during a total eclipse of the Sun that have gone down in history as vindicating Einstein’s (then) new general theory of relativity. I’ve written quite a lot about this in past years, including a little book and a slightly more technical paper. This was a relevant topic for the conference because it wasn’t until general theory of relativity was established as a viable theory of gravity that an explanation could be developed of Slipher’s measurements of galaxy redshifts in terms of an expanding Universe.

2 Comments »

The Importance of Being Homogeneous

Posted in The Universe and Stuff with tags , , , , , , , , on August 29, 2012 by telescoper

A recent article in New Scientist reminded me that I never completed the story I started with a couple of earlier posts (here and there), so while I wait for the rain to stop I thought I’d make myself useful by posting something now. It’s all about a paper available on the arXiv by Scrimgeour et al. concerning the transition to homogeneity of galaxy clustering in the WiggleZ galaxy survey, the abstract of which reads:

We have made the largest-volume measurement to date of the transition to large-scale homogeneity in the distribution of galaxies. We use the WiggleZ survey, a spectroscopic survey of over 200,000 blue galaxies in a cosmic volume of ~1 (Gpc/h)^3. A new method of defining the ‘homogeneity scale’ is presented, which is more robust than methods previously used in the literature, and which can be easily compared between different surveys. Due to the large cosmic depth of WiggleZ (up to z=1) we are able to make the first measurement of the transition to homogeneity over a range of cosmic epochs. The mean number of galaxies N(<r) in spheres of comoving radius r is proportional to r^3 within 1%, or equivalently the fractal dimension of the sample is within 1% of D_2=3, at radii larger than 71 \pm 8 Mpc/h at z~0.2, 70 \pm 5 Mpc/h at z~0.4, 81 \pm 5 Mpc/h at z~0.6, and 75 \pm 4 Mpc/h at z~0.8. We demonstrate the robustness of our results against selection function effects, using a LCDM N-body simulation and a suite of inhomogeneous fractal distributions. The results are in excellent agreement with both the LCDM N-body simulation and an analytical LCDM prediction. We can exclude a fractal distribution with fractal dimension below D_2=2.97 on scales from ~80 Mpc/h up to the largest scales probed by our measurement, ~300 Mpc/h, at 99.99% confidence.

To paraphrase, the conclusion of this study is that while galaxies are strongly clustered on small scales – in a complex `cosmic web’ of clumps, knots, sheets and filaments –  on sufficiently large scales, the Universe appears to be smooth. This is much like a bowl of porridge which contains many lumps, but (usually) none as large as the bowl it’s put in.

Our standard cosmological model is based on the Cosmological Principle, which asserts that the Universe is, in a broad-brush sense, homogeneous (is the same in every place) and isotropic (looks the same in all directions). But the question that has troubled cosmologists for many years is what is meant by large scales? How broad does the broad brush have to be?

I blogged some time ago about that the idea that the  Universe might have structure on all scales, as would be the case if it were described in terms of a fractal set characterized by a fractal dimension D. In a fractal set, the mean number of neighbours of a given galaxy within a spherical volume of radius R is proportional to R^D. If galaxies are distributed uniformly (homogeneously) then D = 3, as the number of neighbours simply depends on the volume of the sphere, i.e. as R^3, and the average number-density of galaxies. A value of D < 3 indicates that the galaxies do not fill space in a homogeneous fashion: D = 1, for example, would indicate that galaxies were distributed in roughly linear structures (filaments); the mass of material distributed along a filament enclosed within a sphere grows linear with the radius of the sphere, i.e. as R^1, not as its volume; galaxies distributed in sheets would have D=2, and so on.

We know that D \simeq 1.2 on small scales (in cosmological terms, still several Megaparsecs), but the evidence for a turnover to D=3 has not been so strong, at least not until recently. It’s just just that measuring D from a survey is actually rather tricky, but also that when we cosmologists adopt the Cosmological Principle we apply it not to the distribution of galaxies in space, but to space itself. We assume that space is homogeneous so that its geometry can be described by the Friedmann-Lemaitre-Robertson-Walker metric.

According to Einstein’s  theory of general relativity, clumps in the matter distribution would cause distortions in the metric which are roughly related to fluctuations in the Newtonian gravitational potential \delta\Phi by \delta\Phi/c^2 \sim \left(\lambda/ct \right)^{2} \left(\delta \rho/\rho\right), give or take a factor of a few, so that a large fluctuation in the density of matter wouldn’t necessarily cause a large fluctuation of the metric unless it were on a scale \lambda reasonably large relative to the cosmological horizon \sim ct. Galaxies correspond to a large \delta \rho/\rho \sim 10^6 but don’t violate the Cosmological Principle because they are too small in scale \lambda to perturb the background metric significantly.

The discussion of a fractal universe is one I’m overdue to return to. In my previous post  I left the story as it stood about 15 years ago, and there have been numerous developments since then, not all of them consistent with each other. I will do a full “Part 2” to that post eventually, but in the mean time I’ll just comment that this particularly one does seem to be consistent with a Universe that possesses the property of large-scale homogeneity. If that conclusion survives the next generation of even larger galaxy redshift surveys then it will come as an immense relief to cosmologists.

The reason for that is that the equations of general relativity are very hard to solve in cases where there isn’t a lot of symmetry; there are just too many equations to solve for a general solution to be obtained.  If the cosmological principle applies, however, the equations simplify enormously (both in number and form) and we can get results we can work with on the back of an envelope. Small fluctuations about the smooth background solution can be handled (approximately but robustly) using a technique called perturbation theory. If the fluctuations are large, however, these methods don’t work. What we need to do instead is construct exact inhomogeneous model, and that is very very hard. It’s of course a different question as to why the Universe is so smooth on large scales, but as a working cosmologist the real importance of it being that way is that it makes our job so much easier than it would otherwise be.

P.S. And I might add that the importance of the Scrimgeour et al paper to me personally is greatly amplified by the fact that it cites a number of my own articles on this theme!

2 Comments »

Is Space Expanding?

Posted in The Universe and Stuff with tags , , , , , , , , , on August 19, 2011 by telescoper

I think I’ve just got time for a quick post this lunchtime, so I’ll pick up on a topic that rose from a series of interchanges on Twitter this morning. As is the case with any interesting exchange of views, this conversation ended up quite some distance from its starting point, and I won’t have time to go all the way back to the beginning, but it was all to do with the “expansion of space“, a phrase one finds all over the place in books articles and web pages about cosmology at both popular and advanced levels.

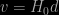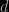What kicked the discussion off was an off-the-cuff humorous remark about the rate at which the Moon is receding from the Earth according to Hubble’s Law; the answer to which is “very slowly indeed”. Hubble’s law is v=H_0 d where v is the apparent recession velocity and d the distance, so for very small distance the speed of expansion is tiny. Strictly speaking, however, the velocity isn’t really observable – what we measure is the redshift, which we then interpret as being due to a velocity.

I chipped in with a comment to the effect that Hubble’s law didn’t apply to the Earth-Moon system (or to the whole Solar System, or for that matter to the Milky Way Galaxy or to the Local Group either) as these are held together by local gravitational effects and do not participate in the cosmic expansion.

To that came the rejoinder that surely these structures are expanding, just very slowly because they are small and that effect is counteracted by motions associated with local structures which “fight against” the “underlying expansion” of space.

But this also makes me uncomfortable, hence this post. It’s not that I think this is necessarily a misconception. The “expansion of space” can be a useful thing to discuss in a pedagogical context. However, as someone once said, teaching physics involves ever-decreasing circles of deception, and the more you think about the language of expanding space the less comfortable you should feel about it, and the more careful you should be in using it as anything other than a metaphor. I’d say it probably belongs to the category of things that Wolfgang Pauli would have described as “not even wrong”, in the sense that it’s more meaningless than incorrect.

Let me briefly try to explain why. In cosmology we assume that the Universe is homogeneous and isotropic and consequently that the space-time is described by the Friedmann-Lemaître-Robertson-Walker metric, which can be written

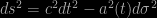
ds^{2} = c^{2} dt^{2}-a^{2}(t) d\sigma^{2}

in which d\sigma^2 describes the (fixed) geometry of a three-dimensional homogeneous space; this spatial part does not depend on time. The imposition of spatial homogeneity selects a preferred time coordinate t, defined such that observers can synchronize watches according to the local density of matter – points in space-time at which the matter density is the same are defined to be at the same time.

The presence of the scale factor 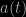a(t) in front of the spatial 3-metric allows the overall 4-metric to change with time, but only in such a way that preserves the spatial geometry, in other words the spatial sections can have different scales at different times, but always have the same shape. It’s a consequence of Einstein’s equations of General Relativity that a Universe described by the FLRW metric must evolve with time (at least in the absence of a cosmological constant). 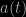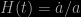In an expanding universe a(t) increases with t and this increase naturally accounts for Hubble’s law, with  H(t)=\dot{a}/a but only if you define velocities and distances in the particular way suggested by the coordinates used.

So how do we interpret this?

Well, there are (at least) two different interpretations depending on your choice of coordinates.  One way to do it is to pick spatial coordinates such that the positions of galaxies change with time; in this choice the redshift of galaxy observed from another is due to their relative motion. Another way to do it is to use coordinates in which the galaxy positions are  fixed; these are called comoving coordinates.  In general relativity we can switch between one view and the other and the observable effect (i.e. the redshift) is the same in either.

Most cosmologists use comoving coordinates (because it’s generally a lot easier that way), and it’s this second interpretation that encourages one to think not about things moving but about space itself expanding. The danger with that is that it sometimes leads one to endow “space” (whatever that means) with physical attributes that it doesn’t really possess. This is most often seen in the analogy of galaxies being the raisins in a pudding, with “space” being the dough that expands as the pudding cooks taking the raisins away from each other. This analogy conveys some idea of the effect of homogeneous expansion, but isn’t really right. Raisins and dough are both made of, you know, stuff. Space isn’t.

In support of my criticism I quote:

 Many semi-popular accounts of cosmology contain statements to the effect that “space itself is swelling up” in causing the galaxies to separate. This seems to imply that all objects are being stretched by some mysterious force: are we to infer that humans who survived for a Hubble time [the age of the universe] would find themselves to be roughly four metres tall? Certainly not….In the common elementary demonstration of the expansion by means of inflating a balloon, galaxies should be represented by glued-on coins, not ink drawings (which will spuriously expand with the universe).

(John Peacock, Cosmological Physics, p. 87-8). A lengthier discussion of this point, which echoes some of the points I make below, can be found here.

To get back to the original point of the question let me add another quote:

A real galaxy is held together by its own gravity and is not free to expand with the universe. Similarly, if [we talk about] the Solar System, Earth, [an] atom, or almost anything, the result would be misleading because most systems are held together by various forces in some sort of equilibrium and cannot partake in cosmic expansion. If we [talk about] clusters of galaxies…most clusters are bound together and cannot expand. Superclusters are vast sprawling systems of numerous clusters that are weakly bound and can expand almost freely with the universe.

(Edward Harrison, Cosmology, p. 278).

I’d put this a different way. The “Hubble expansion” describes the motion of test particles in a the coordinate system I described above, i.e one  which applies to a perfectly homogeneous and isotropic universe. This metric simply doesn’t apply on the scale of the solar system, our own galaxy and even up to the scale of groups or clusters of galaxies. The Andromeda Galaxy (M31),  for example, is not receding from the Milky Way at all – it has a blueshift.  I’d argue that the space-time geometry in such systems is simply nothing like the FLRW form, so one can’t expect to make physical sense trying to to interpret particle motions within them in terms of the usual cosmological coordinate system. Losing the symmetry of the FLRW case  makes the choice of appropriate coordinates much more challenging.

There is cosmic inhomogeneity on even larger scales, of course, but in such cases the “peculiar velocities” generated by the lumpiness can be treated as a (linear) correction to the pure Hubble flow associated with the background cosmology.  In my view, however, in highly concentrated objects that decomposition into an “underlying expansion” and a “local effect” isn’t useful. I’d prefer simply to say that there is no Hubble flow in such objects. To take this to an extreme, what about a black hole? Do you think there’s a Hubble flow inside one of those, struggling to blow it up?

In fact the mathematical task of embedding inhomogeneous structures in an asymptotically FLRW background is not at all straightforward to do exactly, but it is worth mentioning that, by virtue of Birkhoff’s theorem,  the interior of an exactly spherical cavity (i.e. void)  must be described by the (flat) Minkowski metric. In this case the external cosmic expansion has absolutely no effect on the motion of particles in the interior.

I’ll end with this quote from the Fount of All Wisdom, Ned Wright,in response to the question Why doesn’t the Solar System expand if the whole Universe is expanding?

This question is best answered in the coordinate system where the galaxies change their positions. The galaxies are receding from us because they started out receding from us, and the force of gravity just causes an acceleration that causes them to slow down, or speed up in the case of an accelerating expansion. Planets are going around the Sun in fixed size orbits because they are bound to the Sun. Everything is just moving under the influence of Newton’s laws (with very slight modifications due to relativity). [Illustration] For the technically minded, Cooperstock et al. computes that the influence of the cosmological expansion on the Earth’s orbit around the Sun amounts to a growth by only one part in a septillion over the age of the Solar System.

The paper cited in this passage is well worth reading because it demonstrates the importance of the point I was trying to make above about using an appropriate coordinate system:

In the non–spherical case, it is generally recognized that the expansion of the universe does not have observable effects on local physics, but few discussions of this problem in the literature have gone beyond qualitative statements. A serious problem is that these studies were carried out in coordinate systems that are not easily comparable with the frames used for astronomical observations and thus obscure the physical meaning of the computations.

Now I’ve waffled on far too long so  I’ll just finally  recommend this paper entitled Expanding Space: The Root of All Evil and get back to work…

17 Comments »

Einstein and the Eclipse

Posted in Biographical, The Universe and Stuff with tags , , , , , , , on January 4, 2011 by telescoper

Following on from my previous post, I thought you might be interested in this. It’s the last programme in a series called Six Experiments that Changed the World which was presented by the late Ken Campbell. It was made for Channel 4 and first broadcast in 2000. It’s in two parts. If you watch the second one, you might see someone you recognize…


Share/Bookmark

4 Comments »

Black Hole Hunter

Posted in The Universe and Stuff with tags , , , on April 27, 2010 by telescoper

A discussion yesterday with one of my colleagues in the gravitational physics group here in Cardiff gave me the idea of including a little advert here for a fun website called Black Hole Hunter.

The site was developed as a part of the Royal Society Summer Exhibition 2008, Can you hear black holes collide? presented by Cardiff University, and the Universities of Birmingham, Glasgow and Southampton in the UK in collaboration with the Albert Einstein Institute and Milde Marketing in Germany.

The idea is to use your skill, judgement and lugholes to detect the gravitational wave signal from the merger of two black holes in the noisy output of a gravitational wave detector. The image on the left shows the pattern of gravitational radiation as calculated numerically using Einstein’s general theory of relativity. Why not give it a try and see how you get on?

You can play here.

3 Comments »

When Energy Becomes Form

Posted in Art, The Universe and Stuff with tags , , , , , , on February 28, 2010 by telescoper

I’m back in Cardiff, exhausted but, at the same time, rather exhilirated by the past few days in Geneva. Before I crash out I thought I’d update the post I filed a couple of days ago.

On Friday we visited CERN, the highlight of which visit was, for me, seeing the facility where they test the superconducting magnets used in the Large Hadron Collider. We also saw the surface buildings of the ATLAS experiment, but since the LHC was getting ready to rumble again after its winter break we weren’t allowed to see the thing itself, 100 metres below ground. Coincidentally, I learned today that the LHC is now back making collisions once more. Obviously, the practical tips I passed on while I was there did the trick. One likes to help where one can.

The rest of Friday, back in downtown Geneva, was bizarre to say the least. We had the obligatory Swiss dinner of fondue, which is basically a big bowl of melted cheese into which you dip bits of bread repeatedly while hoping that at some point they’re going to bring some proper food. They don’t. To make matters worse we were serenaded by Swiss folk music:  cowbells, alphorns, yodelling – the works. One of the musicians was the spitting image of Dr Evil from the Austin Powers movies but at least there was no sign of Mini-me. I was traumatised by the thought that the world might be brought to a premature end, not by the LHC creating black holes but by excessive yodelling.

After that, as midnight approached, all 24 of us – 8 scientists, 8 artists and 8 architects – gave very short presentations about our work to the others in the hotel lobby area.  I couldn’t do justice to the range of ideas and forms presented there in a short blog like this so I’ll just say it was totally fascinating to listen to these people, see examples of their work, and have the chance to ask questions.

Saturday was the most intense and also the most interesting day. We were housed in a beautiful 19th Century house in the old part of Geneva that used to be the French ambassador’s residence the whole day. Split into various groups we thought, discussed, sketched, scribbled and generally brainstormed our way towards ideas for something to exhibit on our allocated theme. We got together at the end so each group could exchange their ideas with the others. It seemed every group had great fun and there seemed to be some great concepts floating around.

The artist I’m collaborating with is Carlos Garaicoa, who was born in Cuba and who has exhibited his work all over the world. He now shares his time between Havana and Madrid. He showed us examples of his work encompassing a huge range of materials and technologies: video, photography, sculpture – you name it. One of the themes he has been interested in is the idea of documentary matter, meaning objects of various kinds that bear testimony to events or forces acting on them.  Eyal Weizman is the architect Carlos and I will be working with.  He’s a research architect who has, amongst other things, recently completed a long project looking at the construction of the wall that the Israeli government has built in the west bank. 

And then there was me, like a fish out of water. I had looked at the title of the programme, Beyond Entropy: How Energy Becomes Form and decided that it might be interesting to get across the central idea in general relativity, i.e. that gravitational forces can be described in terms of the curvature of space. In my presentation I took this to an extreme and tried to explain how the large-scale structure of the Universe is shaped by small ripples in space in the early Universe that evolve under the action of gravity to produce the structures we see on scales as large as 100 million light years. It seemed to be a good example of gravitational energy becoming form. I summed it up with a quote from John Archibald Wheeler:

Matter tells space how to curve. Space tells matter how to move

Taking cue from these perspectives we had a wide-ranging conversation that took the idea of gravity as an effect of space, and explored this in more general contexts and from different angles. Space is often understood through its boundaries or through the surfaces constraining it and these edges take on a form that represents a sort of diagram of the forces that have acted on it. On a human scale we thought about walls and how the path they follow is shaped not only by topographical constraints but also by socioeconomic considerations. Walls and buildings generally suffer decay or damage too, including catastrophics events like explosions or earthquakes.

We also talked about the relationship between surfaces and the spaces they enclose or divide. The path of a wall such as the west bank barrier is extremely complicated because of the interplay between such factors. It curves in and out seemingly at random, but its shape makes it a document that contains information about the forces that have shaped it. It is a document in itself, not just because it happens to have things written on it in some places!

This thread of discussion got us interested in the possibility of using material objects to reconstruct the history of the processes that formed them: the Moon’s surface offers an example wherein the sequence of impacts can be inferred from the pattern of overlying and underlying craters. This led on to discussions about the relationship between surfaces and volumes generally, taking in holography as a specific example where  two-dimensional object contains three-dimensional volumes.

This all took us quite a long way from the initial riff, but I’m glad of that. My main worry about getting involved in this was that we might end up producing something that was merely didactic, just a fancy metaphorical treatment of basic physics. I wanted to avoid that because I think it would be very boring. I think I shouldn’t have worried that we might head in such a dull direction.

Some of the other groups managed to work up concrete ideas for prototypes to be exhibited. We didn’t really get that far. We were much keener to explore as many concepts as possible before settling on one. For myself, I was just really enjoying the discussion! There are no real constraints on what we can make – within reason of course. Sculptures, plans, buildings, installations, videos, photographs, and even books are all possibilities. It’s quite scary having such a blank canvas. We discussed a number of ways we might develop our discussion into material that can be exhibited but they all need a lot of work to develop, so we’ll carry on our collaboration remotely. I’m quite keen to bring some sort of holographic element into it, and promised to investigate the possibility of making some prototypes.

For the meantime, however,  it’s back to reality for me. A lecture to prepare and give, problem sets to get ready and an exercise class to run, an examination paper to finish writing, and a whole afternoon at the School’s research committee. I wonder if what I’ve been doing over the weekend will count as having “impact”?

2 Comments »

Ninety Years On…

Posted in Books, Talks and Reviews, The Universe and Stuff with tags , , , , , , on May 28, 2009 by telescoper

The 29th May 2009 is a very special day that should be marked by anyone interested in the theory of relativity as it is the 90th anniversary of one of the most famous experiments of all time.

On 29th May 1919, measurements were made during total eclipse of the Sun that have gone down in history as vindicating Einstein’s (then) new general theory of relativity. I’ve written quite a lot about this in past years, including a little book and a slightly more technical paper. I decided, though, to post this little piece that is based on an article I wrote for Firstscience.

The Eclipse that Changed the Universe

A total eclipse of the Sun is a moment of magic: a scant few minutes when our perceptions of the whole Universe are turned on their heads. The Sun’s blinding disc is replaced by ghostly pale tentacles surrounding a black heart – an eerie experience witnessed by hundreds of millions of people throughout Europe and the Near East last August.

But one particular eclipse of the Sun, eighty years ago, challenged not only people’s emotional world. It was set to turn the science of the Universe on its head. For over two centuries, scientists had believed Sir Isaac Newton’s view of the Universe. Now his ideas had been challenged by a young German-Swiss scientist, called Albert Einstein. The showdown – Newton vs Einstein – would be the total eclipse of 29 May 1919.

Newton’s position was set out in his monumental Philosophiae Naturalis Principia Mathematica, published in 1687. The Principia – as it’s familiarly known – laid down a set of mathematical laws that described all forms of motion in the Universe. These rules applied as much to the motion of planets around the Sun as to more mundane objects like apples falling from trees.

At the heart of Newton’s concept of the Universe were his ideas about space and time. Space was inflexible, laid out in a way that had been described by the ancient Greek mathematician Euclid in his laws of geometry. To Newton, space was the immovable and unyielding stage on which bodies acted out their motions. Time was also absolute, ticking away inexorably at the same rate for everyone in the Universe.

Sir Isaac Newton
Sir Isaac Newton by Sir Godfrey Kneller
Courtesy of the National Portrait Gallery, London Sir Isaac Newton proposed the first theory of gravity.

For over 200 years, scientists saw the Cosmos through Newton’s eyes. It was a vast clockwork machine, evolving by predetermined rules through regular space, against the beat of an absolute clock. This edifice totally dominated scientific thought, until it was challenged by Albert Einstein.

In 1905, Einstein dispensed with Newton’s absolute nature of space and time. Although born in Germany, during this period of his life he was working as a patent clerk in Berne, Switzerland. He encapsulated his new ideas on motion, space and time in his special theory of relativity. But it took another ten years for Einstein to work out the full consequences of his ideas, including gravity. The general theory of relativity, first aired in 1915, was as complete a description of motion as Newton had prescribed in his Principia. But Einstein’s description of gravity required space to be curved. Whereas for Newton space was an inflexible backdrop, for Einstein it had to bend and flex near massive bodies. This warping of space, in turn, would be responsible for guiding objects such as planets along their orbits.

Einstein and Eddington
Royal Observatory Greenwich Albert Einstein and Arthur Eddington: the father of relativity and the man who proved him right.

By the time he developed his general theory, Einstein was back in Germany, working in Berlin. But a copy of his general theory of relativity was soon smuggled through war-torn Europe to Cambridge. There it was read by Arthur Stanley Eddington, Britain’s leading astrophysicist. Eddington realised that Einstein’s theory could be tested. If space really was distorted by gravity, then light passing through it would not travel in a straight line, but would follow a curved path. The stronger the force of gravity, the more the light would be bent. The bending would be largest for light passing very close to a very massive body, such as the Sun.

Unfortunately, the most massive objects known to astronomers at the time were also very bright. This was before black holes were seriously considered, and stars provided the strongest gravitational fields known. The Sun was particularly useful, being a star right on our doorstep. But it is impossible to see how the light from faint background stars might be bent by the Sun’s gravity, because the Sun’s light is so bright it completely swamps the light from objects beyond it.

Click here for enlarged version
Royal Observatory Greenwich Scientist’s sketch of the path of the vital 1919 eclipse.

Eddington realised the solution. Observe during a total eclipse, when the Sun’s light is blotted out for a few minutes, and you can see distant stars that appear close to the Sun in the sky. If Einstein was right, the Sun’s gravity would shift these stars to slightly different positions, compared to where they are seen in the night sky at other times of the year when the Sun far away from them. The closer the star appears to the Sun during totality, the bigger the shift would be.

Eddington began to put pressure on the British scientific establishment to organise an experiment. The Astronomer Royal of the time, Sir Frank Watson Dyson, realised that the 1919 eclipse was ideal. Not only was totality unusually long (around six minutes, compared with the two minutes we experienced in 1999) but during totality the Sun would be right in front of the Hyades, a cluster of bright stars.

But at this point the story took a twist. Eddington was a Quaker and, as such, a pacifist. In 1917, after disastrous losses during the Somme offensive, the British government introduced conscription to the armed forces. Eddington refused the draft and was threatened with imprisonment. In the end, Dyson’s intervention was crucial persuading the government to spare Eddington. His conscription was postponed under the condition that, if the war had finished by 1919, Eddington himself would lead an expedition to measure the bending of light by the Sun. The rest, as they say, is history.

The path of totality of the 1919 eclipse passed from northern Brazil, across the Atlantic Ocean to West Africa. In case of bad weather (amongst other reasons) two expeditions were organised: one to Sobral, in Brazil, and the other to the island of Principe, in the Gulf of Guinea close to the West African coast. Eddington himself went to Principe; the expedition to Sobral was led by Andrew Crommelin from the Royal Observatory at Greenwich.

Click for enlarged version
Royal Observatory Greenwich British scientists in the field at Sobral in 1919.

The expeditions did not go entirely according to plan. When the day of the eclipse (29 May) dawned on Principe, Eddington was greeted with a thunderstorm and torrential rain. By mid-afternoon the skies had partly cleared and he took some pictures through cloud.

Meanwhile, at Sobral, Crommelin had much better weather – but he had made serious errors in setting up his equipment. He focused his main telescope the night before the eclipse, but did not allow for the distortions that would take place as the temperature climbed during the day. Luckily, he had taken a backup telescope along, and this in the end provided the best results of all.

After the eclipse, Eddington himself carefully measured the positions of the stars that appeared near the Sun’s eclipsed image, on the photographic plates exposed at both Sobral and Principe. He then compared them with reference positions taken previously when the Hyades were visible in the night sky. The measurements had to be incredibly accurate, not only because the expected deflections were small. The images of the stars were also quite blurred, because of problems with the telescopes and because they were seen through the light of the Sun’s glowing atmosphere, the solar corona.

Before long the results were ready. Britain’s premier scientific body, the Royal Society, called a special meeting in London on 6 November. Dyson, as Astronomer Royal took the floor, and announced that the measurements did not support Newton’s long-accepted theory of gravity. Instead, they agreed with the predictions of Einstein’s new theory.

Image from Sobral
Royal Observatory Greenwich The final proof: the small red line shows how far the position of the star has been shifted by the Sun’s gravity.

The press reaction was extraordinary. Einstein was immediately propelled onto the front pages of the world’s media and, almost overnight, became a household name. There was more to this than purely the scientific content of his theory. After years of war, the public embraced a moment that moved mankind from the horrors of destruction to the sublimity of the human mind laying bare the secrets of the Cosmos. The two pacifists in the limelight – the British Eddington and the German-born Einstein – were particularly pleased at the reconciliation between their nations brought about by the results.

But the popular perception of the eclipse results differed quite significantly from the way they were viewed in the scientific establishment. Physicists of the day were justifiably cautious. Eddington had needed to make significant corrections to some of the measurements, for various technical reasons, and in the end decided to leave some of the Sobral data out of the calculation entirely. Many scientists were suspicious that he had cooked the books. Although the suspicion lingered for years in some quarters, in the end the results were confirmed at eclipse after eclipse with higher and higher precision.

Image from Hubble

NASA In this cosmic ‘gravitational lens,’ a huge cluster of galaxies distorts the light from more distant galaxies into a pattern of giant arcs.

Nowadays astronomers are so confident of Einstein’s theory that they rely on the bending of light by gravity to make telescopes almost as big as the Universe. When the conditions are right, gravity can shift an object’s position by far more than a microscopic amount. The ideal situation is when we look far out into space, and centre our view not on an individual star like the Sun, but on a cluster of hundreds of galaxies – with a total mass of perhaps 100 million million suns. The space-curvature of this immense ‘gravitational lens’ can gather the light from more remote objects, and focus them into brilliant curved arcs in the sky. From the size of the arcs, astronomers can ‘weigh’ the cluster of galaxies.

Einstein didn’t live long enough to see through a gravitational lens, but if he had he would definitely have approved….

19 Comments »

« Older Entries
Newer Entries »