Once again, it’s time for a quick update of activity at the Open Journal of Astrophysics. This week we have published another batch of four papers which takes the count in Volume 7 (2024) up to 77 and the total published altogether by OJAp up to 192. Things are picking up again after the summer lull, and we’re moving towards a double century. If we keep up a steady average of four per week we’ll be at 200 per year.
In chronological order, the four papers published this week, with their overlays, are as follows. You can click on the images of the overlays to make them larger should you wish to do so.
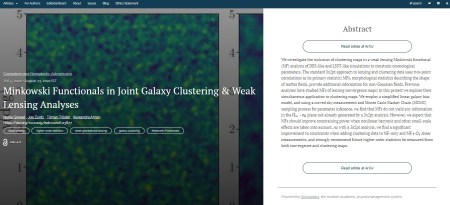
First one up is “Quasi-two-dimensionality of three-dimensional, magnetically dominated, decaying turbulence” by Shreya Dwivedi, Chandranathan Anandavijayan, and Pallavi Bhat of TIFR, Bangalore, India. The paper presents an analysis of numerical simulations of MHD turbulence using Minkowski Functionals, with implications for local anisotropies revealed therein. It was published on 9th September 2024 and is in the folder marked High-Energy Astrophysical Phenomena.
Here is a screen grab of the overlay, which includes the abstract:
You can find the officially accepted version of the paper on the arXiv here.
The second paper to announce, also published on 9th September 2024, is “mochi_class: Modelling Optimisation to Compute Horndeski In class” by Matteo Cataneo (Universität Bonn, Germany) and Emilio Bellini (SISSA, Trieste, Italy). This article presents a cosmological Einstein-Boltzmann solver adapted to work with Horndeski gravity, together with validation tests. It is in the folder Cosmology and NonGalactic Astrophysics.
You can see the overlay here:
The accepted version of this paper can be found on the arXiv here.
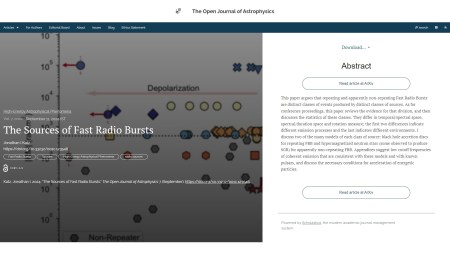
The third paper, published on 11th September 2024 in the folder marked High-Energy Astrophysical Phenomena, is by Jonathan Katz of Washington University, St Louis, USA. The title is “The Sources of Fast Radio Bursts” and it presents a discussion of the possible physical origin of Fast Radio Bursts, arguing that they fall into two distinct groups.
The final version accepted on arXiv is here.
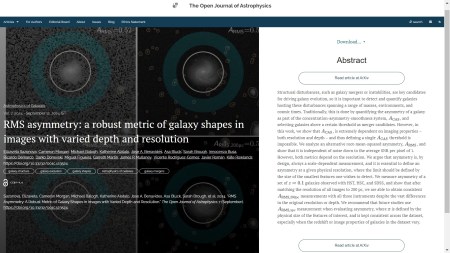
Last in this batch, but by no means least, is “RMS asymmetry: a robust metric of galaxy shapes in images with varied depth and resolution” by Elizaveta Sazonova (U. Waterloo, Canada) with 15 other authors spread around the world (in Canada, USA, Australia, Italy, Chile, UK, Poland, Mexico, Germany, and Spain). This paper presents a method of quantifying distortion of galaxy images connected with mergers or other instabilities. It is in the folder marked Astrophysics of Galaxies and was published on September 12th 2024 with this overlay:
You can find the official accepted version on the arXiv here.
That’s all for now. I will post another update in a week.