Archive for Cosmology

« Older Entries
Newer Entries »

Why the Big Bang wasn’t as loud as you think…

Posted in The Universe and Stuff with tags , , , , , on March 31, 2015 by telescoper

So how loud was the Big Bang?

I’ve posted on this before but a comment posted today reminded me that perhaps I should recycle it and update it as it relates to the cosmic microwave background, which is what I work on on the rare occasions on which I get to do anything interesting.

As you probably know the Big Bang theory involves the assumption that the entire Universe – not only the matter and energy but also space-time itself – had its origins in a single event a finite time in the past and it has been expanding ever since. The earliest mathematical models of what we now call the  Big Bang were derived independently by Alexander Friedman and George Lemaître in the 1920s. The term “Big Bang” was later coined by Fred Hoyle as a derogatory description of an idea he couldn’t stomach, but the phrase caught on. Strictly speaking, though, the Big Bang was a misnomer.

Friedman and Lemaître had made mathematical models of universes that obeyed the Cosmological Principle, i.e. in which the matter was distributed in a completely uniform manner throughout space. Sound consists of oscillating fluctuations in the pressure and density of the medium through which it travels. These are longitudinal “acoustic” waves that involve successive compressions and rarefactions of matter, in other words departures from the purely homogeneous state required by the Cosmological Principle. The Friedman-Lemaitre models contained no sound waves so they did not really describe a Big Bang at all, let alone how loud it was.

However, as I have blogged about before, newer versions of the Big Bang theory do contain a mechanism for generating sound waves in the early Universe and, even more importantly, these waves have now been detected and their properties measured.

Planck_CMB

The above image shows the variations in temperature of the cosmic microwave background as charted by the Planck Satellite. The average temperature of the sky is about 2.73 K but there are variations across the sky that have an rms value of about 0.08 milliKelvin. This corresponds to a fractional variation of a few parts in a hundred thousand relative to the mean temperature. It doesn’t sound like much, but this is evidence for the existence of primordial acoustic waves and therefore of a Big Bang with a genuine “Bang” to it.

A full description of what causes these temperature fluctuations would be very complicated but, roughly speaking, the variation in temperature you corresponds directly to variations in density and pressure arising from sound waves.

So how loud was it?

The waves we are dealing with have wavelengths up to about 200,000 light years and the human ear can only actually hear sound waves with wavelengths up to about 17 metres. In any case the Universe was far too hot and dense for there to have been anyone around listening to the cacophony at the time. In some sense, therefore, it wouldn’t have been loud at all because our ears can’t have heard anything.

Setting aside these rather pedantic objections – I’m never one to allow dull realism to get in the way of a good story- we can get a reasonable value for the loudness in terms of the familiar language of decibels. This defines the level of sound (L) logarithmically in terms of the rms pressure level of the sound wave Prms relative to some reference pressure level Pref

L=20 log10[Prms/Pref].

(the 20 appears because of the fact that the energy carried goes as the square of the amplitude of the wave; in terms of energy there would be a factor 10).

There is no absolute scale for loudness because this expression involves the specification of the reference pressure. We have to set this level by analogy with everyday experience. For sound waves in air this is taken to be about 20 microPascals, or about 2×10-10 times the ambient atmospheric air pressure which is about 100,000 Pa.  This reference is chosen because the limit of audibility for most people corresponds to pressure variations of this order and these consequently have L=0 dB. It seems reasonable to set the reference pressure of the early Universe to be about the same fraction of the ambient pressure then, i.e.

Pref~2×10-10 Pamb.

The physics of how primordial variations in pressure translate into observed fluctuations in the CMB temperature is quite complicated, because the primordial universe consists of a plasma rather than air. Moreover, the actual sound of the Big Bang contains a mixture of wavelengths with slightly different amplitudes. In fact here is the spectrum, showing a distinctive signature that looks, at least in this representation, like a fundamental tone and a series of harmonics…

Planck_power_spectrum_orig

 

If you take into account all this structure it all gets a bit messy, but it’s quite easy to get a rough but reasonable estimate by ignoring all these complications. We simply take the rms pressure variation to be the same fraction of ambient pressure as the averaged temperature variation are compared to the average CMB temperature,  i.e.

Prms~ a few ×10-5Pamb.

If we do this, scaling both pressures in logarithm in the equation in proportion to the ambient pressure, the ambient pressure cancels out in the ratio, which turns out to be a few times 10-5. With our definition of the decibel level we find that waves of this amplitude, i.e. corresponding to variations of one part in a hundred thousand of the reference level, give roughly L=100dB while part in ten thousand gives about L=120dB. The sound of the Big Bang therefore peaks at levels just a bit less than 120 dB.

cooler_decibel_chart

As you can see in the Figure above, this is close to the threshold of pain,  but it’s perhaps not as loud as you might have guessed in response to the initial question. Modern popular beat combos often play their dreadful rock music much louder than the Big Bang….

A useful yardstick is the amplitude  at which the fluctuations in pressure are comparable to the mean pressure. This would give a factor of about 1010 in the logarithm and is pretty much the limit that sound waves can propagate without distortion. These would have L≈190 dB. It is estimated that the 1883 Krakatoa eruption produced a sound level of about 180 dB at a range of 100 miles. By comparison the Big Bang was little more than a whimper.

PS. If you would like to read more about the actual sound of the Big Bang, have a look at John Cramer’s webpages. You can also download simulations of the actual sound. If you listen to them you will hear that it’s more of  a “Roar” than a “Bang” because the sound waves don’t actually originate at a single well-defined event but are excited incoherently all over the Universe.

4 Comments »

Forthcoming Attraction: Dark Energy and its Discontents

Posted in Talks and Reviews, The Universe and Stuff with tags , , on March 11, 2015 by telescoper

Busy again today, so just time for a spot of gratuitous self-promotion. I shall be giving a public lecture on Friday 24th April 2015 at the very posh-sounding Bath Royal Literary and Scientific Institution. Here is the poster, which explains all. Will I see any readers of this blog there?

Bath_lecture

7 Comments »

Parametric Resonance – It Don’t Mean A Thing If It Ain’t Got That Swing

Posted in The Universe and Stuff with tags , , , on March 10, 2015 by telescoper

It’s a small universe world. This  lunchtime I turned up to the local Cosmology discussion group for a talk on reheating after inflation during which the topic of parametric resonance came up. To illustrate the concept the speaker showed this nice video, and there was my esteemed former University of Nottingham colleague and fellow jazz enthusiast Roger Bowley explaining all!

 

 

Leave a comment »

Four Times a Supernova

Posted in The Universe and Stuff with tags , , , , on March 9, 2015 by telescoper

I’ve been a bit pressed for time recently (to put it mildly) so am a bit late catching up on a wonderful observation (by Kelly et al.) reported in last week’s issue of Science. Here’s the abstract:

In 1964, Refsdal hypothesized that a supernova whose light traversed multiple paths around a strong gravitational lens could be used to measure the rate of cosmic expansion. We report the discovery of such a system. In Hubble Space Telescope imaging, we have found four images of a single supernova forming an Einstein cross configuration around a redshift z = 0.54 elliptical galaxy in the MACS J1149.6+2223 cluster. The cluster’s gravitational potential also creates multiple images of the z = 1.49 spiral supernova host galaxy, and a future appearance of the supernova elsewhere in the cluster field is expected. The magnifications and staggered arrivals of the supernova images probe the cosmic expansion rate, as well as the distribution of matter in the galaxy and cluster lenses.

And here’s a nice picture of the system which I ripped of from a nice report in Physics World:

PW-2015-03-05-Commissariat-supernovae

Multiple images of background objects caused by gravitational lensing have been observed before, but the key thing about this particular “Einstein Cross” is that the background object is a type of exploding star called a supernova. That means that the light it emits will decay over time. That light reaches us via four different paths around the intervening galaxy cluster so monitoring the different evolution in the four images will yield direct measurements of the physical scale of the cluster and hopefully  answer a host of interesting cosmological questions.

Leave a comment »

That Big Black Hole Story

Posted in The Universe and Stuff with tags , , , , , , , , on February 28, 2015 by telescoper

There’s been a lot of news coverage this week about a very big black hole, so I thought I’d post a little bit of background.  The paper describing the discovery of the object concerned appeared in Nature this week, but basically it’s a quasar at a redshift z=6.30. That’s not the record for such an object. Not long ago I posted an item about the discovery of a quasar at redshift 7.085, for example. But what’s interesting about this beastie is that it’s a very big beastie, with a central black hole estimated to have a mass of around 12 billion times the mass of the Sun, which is a factor of ten or more larger than other objects found at high redshift.

Anyway, I thought perhaps it might be useful to explain a little bit about what difficulties this observation might pose for the standard “Big Bang” cosmological model. Our general understanding of galaxies form is that gravity gathers cold non-baryonic matter into clumps  into which “ordinary” baryonic material subsequently falls, eventually forming a luminous galaxy forms surrounded by a “halo” of (invisible) dark matter.  Quasars are galaxies in which enough baryonic matter has collected in the centre of the halo to build a supermassive black hole, which powers a short-lived phase of extremely high luminosity.

The key idea behind this picture is that the haloes form by hierarchical clustering: the first to form are small but  merge rapidly  into objects of increasing mass as time goes on. We have a fairly well-established theory of what happens with these haloes – called the Press-Schechter formalism – which allows us to calculate the number-density N(M,z) of objects of a given mass M as a function of redshift z. As an aside, it’s interesting to remark that the paper largely responsible for establishing the efficacy of this theory was written by George Efstathiou and Martin Rees in 1988, on the topic of high redshift quasars.

Anyway, this is how the mass function of haloes is predicted to evolve in the standard cosmological model; the different lines show the distribution as a function of redshift for redshifts from 0 (red) to 9 (violet):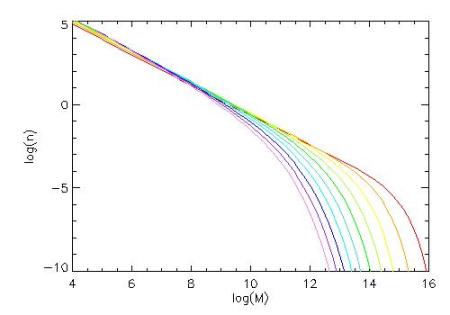

Note   that the typical size of a halo increases with decreasing redshift, but it’s only at really high masses where you see a really dramatic effect. The plot is logarithmic, so the number density large mass haloes falls off by several orders of magnitude over the range of redshifts shown. The mass of the black hole responsible for the recently-detected high-redshift quasar is estimated to be about 1.2 \times 10^{10} M_{\odot}. But how does that relate to the mass of the halo within which it resides? Clearly the dark matter halo has to be more massive than the baryonic material it collects, and therefore more massive than the central black hole, but by how much?

This question is very difficult to answer, as it depends on how luminous the quasar is, how long it lives, what fraction of the baryons in the halo fall into the centre, what efficiency is involved in generating the quasar luminosity, etc.   Efstathiou and Rees argued that to power a quasar with luminosity of order 10^{13} L_{\odot} for a time order 10^{8} years requires a parent halo of mass about 2\times 10^{11} M_{\odot}.  Generally, i’s a reasonable back-of-an-envelope estimate that the halo mass would be about a hundred times larger than that of the central black hole so the halo housing this one could be around 10^{12} M_{\odot}.

You can see from the abundance of such haloes is down by quite a factor at redshift 7 compared to redshift 0 (the present epoch), but the fall-off is even more precipitous for haloes of larger mass than this. We really need to know how abundant such objects are before drawing definitive conclusions, and one object isn’t enough to put a reliable estimate on the general abundance, but with the discovery of this object  it’s certainly getting interesting. Haloes the size of a galaxy cluster, i.e.  10^{14} M_{\odot}, are rarer by many orders of magnitude at redshift 7 than at redshift 0 so if anyone ever finds one at this redshift that would really be a shock to many a cosmologist’s  system, as would be the discovery of quasars with such a high mass  at  redshifts significantly higher than seven.

Another thing worth mentioning is that, although there might be a sufficient number of potential haloes to serve as hosts for a quasar, there remains the difficult issue of understanding precisely how the black hole forms and especially how long it takes to do so. This aspect of the process of quasar formation is much more complicated than the halo distribution, so it’s probably on detailed models of  black-hole  growth that this discovery will have the greatest impact in the short term.

1 Comment »

What is the Scientific Method?

Posted in The Universe and Stuff with tags , , on February 25, 2015 by telescoper

Twitter sent me this video about the scientific method yesterday, so I thought I’d share it via this blog.

The term Scientific Method is one that I find it difficult to define satisfactorily, despite having worked in science for over 25 years. The Oxford English Dictionary  defines Scientific Method as

..a method or procedure that has characterized natural science since the 17th century, consisting in systematic observation, measurement, and experiment, and the formulation, testing, and modification of hypotheses.

This is obviously a very general description, and the balance between the different aspects described is very different in different disciplines. For this reason when people try to define what the Scientific Method is for their own field, it doesn’t always work for others even within the same general area. It’s fairly obvious that zoology is very different from nuclear physics, but that doesn’t mean that either has to be unscientific. Moreover, the approach used in laboratory-based experimental physics can be very different from that used in astrophysics, for example. What I like about this video, though, is that it emphasizes the role of uncertainty in how the process works. I think that’s extremely valuable, as the one thing that I think should define the scientific method across all disciplines is a proper consideration of the assumptions made, the possibility of experimental error, and the limitations of what has been done. I wish this aspect of science had more prominence in media reports of scientific breakthroughs. Unfortunately these are almost always presented as certainties, so if they later turn out to be incorrect it looks like science itself has gone wrong. I don’t blame the media entirely about this, as there are regrettably many scientists willing to portray their own findings in this way.

When I give popular talks about my own field, Cosmology,  I often  look for appropriate analogies or metaphors in television programmes about forensic science, such as CSI: Crime Scene Investigation which I used to watch quite regularly (to the disdain of many of my colleagues and friends). Cosmology is methodologically similar to forensic science because it is generally necessary in both these fields to proceed by observation and inference, rather than experiment and deduction: cosmologists have only one Universe;  forensic scientists have only one scene of the crime. They can collect trace evidence, look for fingerprints, establish or falsify alibis, and so on. But they can’t do what a laboratory physicist or chemist would typically try to do: perform a series of similar experimental crimes under slightly different physical conditions. What we have to do in cosmology is the same as what detectives do when pursuing an investigation: make inferences and deductions within the framework of a hypothesis that we continually subject to empirical test. This process carries on until reasonable doubt is exhausted, if that ever happens. Of course there is much more pressure on detectives to prove guilt than there is on cosmologists to establish “the truth” about our Cosmos. That’s just as well, because there is still a very great deal we do not know about how the Universe works.

 

 

2 Comments »

When random doesn’t seem random..

Posted in Crosswords, The Universe and Stuff with tags , , , , , on February 21, 2015 by telescoper

A few months have passed since I last won a dictionary as a prize in the Independent Crossword competition. That’s nothing remarkable in itself, but since my average rate of dictionary accumulation has been about one a month over the last few years, it seems a bit of a lull.  Have I forgotten how to do crosswords and keep sending in wrong solutions? Is the Royal Mail intercepting my post? Has the number of correct entries per week suddenly increased, reducing my odds of winning? Have the competition organizers turned against me?

In fact, statistically speaking, there’s nothing significant in this gap. Even if my grids are all correct, the number of correct grids has remained constant, and the winner is pulled at random  from those submitted (i.e. in such a way that all correct entries are equally likely to be drawn) , then a relatively long unsuccessful period such as I am experiencing at the moment is not at all improbable. The point is that such runs are far more likely in a truly random process than most people imagine, as indeed are runs of successes. Chance coincidences happen more often than you think.

I try this out in lectures sometimes, by asking a member of the audience to generate a random sequence of noughts and ones in their head. It seems people are very conscious that the number of ones should be roughly equal to the number of noughts that they impose that as they go along. Almost universally, the supposedly random sequences people produce only have very short runs of 1s or 0s because, say, a run like ‘00000’ just seems too unlikely. Well, it is unlikely, but that doesn’t mean it won’t happen. In a truly random binary sequence like this (i.e. one in which 1 and 0 both have a probability of 0.5 and each selection is independent of the others), coincidental runs of consecutive 0s and 1s happen with surprising frequency. Try it yourself, with a coin.

Coincidentally, the subject of randomness was suggested to me independently yesterday by an anonymous email correspondent by the name of John Peacock as I have blogged about it before; one particular post on this topic is actually one of this blog’s most popular articles).  What triggered this was a piece about music players such as Spotify (whatever that is) which have a “random play” feature. Apparently people don’t accept that it is “really random” because of the number of times the same track comes up. To deal with this “problem”, experts are working at algorithms that don’t actually play things randomly but in such a way that accords with what people think randomness means.

I think this fiddling is a very bad idea. People understand probability so poorly anyway that attempting to redefine the word’s meaning is just going to add confusion. You wouldn’t accept a casino that used loaded dice, so why allow cheating in another context? Far better for all concerned for the general public to understand what randomness is and, perhaps more importantly, what it looks like.

I have to confess that I don’t really like the word “randomness”, but I haven’t got time right now for a rant about it. There are, however, useful mathematical definitions of randomness and it is also (sometimes) useful to make mathematical models that display random behaviour in a well-defined sense, especially in situations where one has to take into account the effects of noise.

I thought it would be fun to illustrate one such model. In a point process, the random element is a “dot” that occurs at some location in time or space. Such processes can be defined in one or more dimensions and relate to a wide range of situations: arrivals of buses at a bus stop, photons in a detector, darts on a dartboard, and so on.

The statistical description of clustered point patterns is a fascinating subject, because it makes contact with the way in which our eyes and brain perceive pattern. I’ve spent a large part of my research career trying to figure out efficient ways of quantifying pattern in an objective way and I can tell you it’s not easy, especially when the data are prone to systematic errors and glitches. I can only touch on the subject here, but to see what I am talking about look at the two patterns below:

pointbpointa

You will have to take my word for it that one of these is a realization of a two-dimensional Poisson point process and the other contains correlations between the points. One therefore has a real pattern to it, and one is a realization of a completely unstructured random process.

I show this example in popular talks and get the audience to vote on which one is the random one. In fact, I did this just a few weeks ago during a lecture in our module Quarks to Cosmos, which attempts to explain scientific concepts to non-science students. As usual when I do this, I found that the vast majority thought  that the top one is random and the bottom one is the one with structure to it. It is not hard to see why. The top pattern is very smooth (what one would naively expect for a constant probability of finding a point at any position in the two-dimensional space) , whereas the bottom one seems to offer a profusion of linear, filamentary features and densely concentrated clusters.

In fact, it’s the bottom  picture that was generated by a Poisson process using a  Monte Carlo random number generator. All the structure that is visually apparent in the second example is imposed by our own sensory apparatus, which has evolved to be so good at discerning patterns that it finds them when they’re not even there!

The top  process is also generated by a Monte Carlo technique, but the algorithm is more complicated. In this case the presence of a point at some location suppresses the probability of having other points in the vicinity. Each event has a zone of avoidance around it; the points are therefore anticorrelated. The result of this is that the pattern is much smoother than a truly random process should be. In fact, this simulation has nothing to do with galaxy clustering really. The algorithm used to generate it was meant to mimic the behaviour of glow-worms which tend to eat each other if they get  too close. That’s why they spread themselves out in space more uniformly than in the “really” random pattern.

I assume that Spotify’s non-random play algorithm will have the effect of producing a one-dimensional version of the top pattern, i.e. one with far too few coincidences to be genuinely random.

Incidentally, I got both pictures from Stephen Jay Gould’s collection of essays Bully for Brontosaurus and used them, with appropriate credit and copyright permission, in my own book From Cosmos to Chaos.

The tendency to find things that are not there is quite well known to astronomers. The constellations which we all recognize so easily are not physical associations of stars, but are just chance alignments on the sky of things at vastly different distances in space. That is not to say that they are random, but the pattern they form is not caused by direct correlations between the stars. Galaxies form real three-dimensional physical associations through their direct gravitational effect on one another.

People are actually pretty hopeless at understanding what “really” random processes look like, probably because the word random is used so often in very imprecise ways and they don’t know what it means in a specific context like this.  The point about random processes, even simpler ones like repeated tossing of a coin, is that coincidences happen much more frequently than one might suppose.

I suppose there is an evolutionary reason why our brains like to impose order on things in a general way. More specifically scientists often use perceived patterns in order to construct hypotheses. However these hypotheses must be tested objectively and often the initial impressions turn out to be figments of the imagination, like the canals on Mars.

Perhaps I should complain to WordPress about the widget that links pages to a “random blog post”. I’m sure it’s not really random….

10 Comments »

A First Author Paper

Posted in The Universe and Stuff with tags , , , , , on February 16, 2015 by telescoper

I thought I’d take a few minutes to celebrate the fact that the first first-author paper by my PhD student here at the University of Sussex, Mateja Gosenca, has just hit the arXiv. The abstract reads:

We explore the dynamical behaviour of cosmological models involving a scalar field (with an exponential potential and a canonical kinetic term) and a matter fluid with spatial curvature included in the equations of motion. Using appropriately defined parameters to describe the evolution of the scalar field energy in this situation, we find that there are two extra fixed points that are not present in the case without curvature. We also analyse the evolution of the effective equation-of-state parameter for different initial values of the curvature.

There has been a lot of interest recently in treating cosmological models as dynamical systems, and the class of models we studied has been analysed before (see the references in the paper) but this paper addresses them in a different (and perhaps slightly more elegant) way and in the context of quintessence models for dark energy. It also contains some very pretty multi-dimensional phase portraits, like this:

Mateja

Of course these figures are self-explanatory, so I’ll say no more about them…

6 Comments »

Planck Update

Posted in The Universe and Stuff with tags , , , , on February 5, 2015 by telescoper

Just time for a very quick post today to pass on thhe news that most of the 2015 crop of papers from the Planck mission have now been released and are available to download here. You can also find some related data products here.

I haven’t had time to look at these in any detail myself, but my attention was drawn (in the light of the recently-released combined analysis of Planck and Bicpe2/Keck data) to the constraints on inflationary cosmological models shown in this figure:

inflation

It seems that the once-popular (because it is simple) m^2 \phi^2 model of inflation is excluded at greater than 99% confidence…

Feel free to add reactions to any of the papers in the new release via the comments box!

4 Comments »

The BICEP2 Bubble Bursts…

Posted in The Universe and Stuff with tags , , , , on January 30, 2015 by telescoper

I think it’s time to break the worst-kept secret in cosmology, concerning the claimed detection of primordial gravitational waves by the BICEP2 collaboration that caused so much excitement last year; see this blog, passim. If you recall, the biggest uncertainty in this result derived from the fact that it was made at a single frequency, 150 GHz, so it was impossible to determine the spectrum of the signal. Since dust in our own galaxy emits polarized light in the far-infrared there was no direct evidence to refute the possibility that this is what BICEP2 had detected. The indirect arguments presented by the BICEP2 team (that there should be very little dust emission in the region of the sky they studied) were challenged, but the need for further measurements was clear.

Over the rest of last year, the BICEP2 team collaborated with the consortium working on the Planck satellite, which has measurements over the whole sky at a wide range of frequencies. Of particular relevance to the BICEP2 controversy are the Planck mesurements at such high frequency that they are known to be dominated by dust emission, specifically the 353 GHz channel. Cross-correlating these data with the BICEP2 measurements (and also data from the Keck Array which is run by the same team) should allow the identification of that part of the BICEP2 signal that is due to dust emission to be isolated and subtracted. What’s left would be the bit that’s interesting for cosmology. This is the work that has been going on, the results of which will officially hit the arXiv next week.

However, news has been leaking out over the last few weeks about what the paper will say. Being the soul of discretion I decided not to blog about these rumours. However, yesterday I saw the killer graph had been posted so I’ve decided to share it here:

cross-correlation

The black dots with error bars show the original BICEP/Keck “detection” of B-mode polarization which they assumed was due to primordial gravitational waves. The blue dots with error bars show the results after subtracting the correlated dust component. There is clearly a detection of B-mode polarization. However, the red curve shows the B-mode polarization that’s expected to be generated not by primordial gravitational waves but by gravitational lensing; this signal is already known. There’s a slight hint of an excess over the red curve at multipoles of order 200, but it is not statistically significant. Note that the error bars are larger when proper uncertainties are folded in.

Here’s a quasi-official statement of the result (orginall issued in French) that has been floating around on Twitter:

BICEP_null

To be blunt, therefore, the BICEP2 measurement is a null result for primordial gravitational waves. It’s by no means a proof that there are no gravitational waves at all, but it isn’t a detection. In fact, for the experts, the upper limit on the tensor-to-scalar ratio  R from this analysis is R<0.13 at 95% confidences there’s actually till room for a sizeable contribution from gravitational waves, but we haven’t found it yet.

The search goes on…

UPDATE: As noted below in the comments, the actual paper has now been posted online here along with supplementary materials. I’m not surprised as the cat is already well and truly out of the bag, with considerable press interest, some of it driving traffic here!

UPDATE TO THE UPDATE: There’s a news item in Physics World and another in Nature News about this, both with comments from me and others.

43 Comments »

« Older Entries
Newer Entries »